数组/字符串
88. 合并两个有序数组
能想到是要使用双指针,但具体的实现细节没有想明白。
想到避免使用额外空间解决问题,但没有想出具体方案。
双指针有两种遍历方向,为什么要选择由后至前遍历呢? 若是由前向后遍历,遇到2>1的情况时,1中的元素会被覆盖。

几个细节: 1.针对于2数组大小大于1数组的情况,可以采用先比较1>2的情况,剩下走else分支。
2.注意p1是否越界的条件应该写在大小判断之前,否则会导致索引越界。
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p1=m-1;
int p2=n-1;
int p=m+n-1;
while(p2>=0){
if (p1>=0 &&nums1[p1]>nums2[p2]){
nums1[p--]=nums1[p1--];
}
else{
nums1[p--]=nums2[p2--];
}
}
}
};
LCR 120. 寻找文件副本
思路1: 一来想到的就是利用双指针来做,但不知到为何报错?
但后来知道这种题目暗指一定有返回数值的题,可以返回-1来占空。
注意排序函数的书写:
sort(vec.begin(),vec.end());
思路2: 哈希表

class Solution {
public:
int findRepeatDocument(vector<int>& documents) {
unordered_map<int, bool> map;
for(int doc : documents) {
if(map[doc]) return doc;
map[doc] = true;
}
return -1;
}
};
思路3:
原地交换
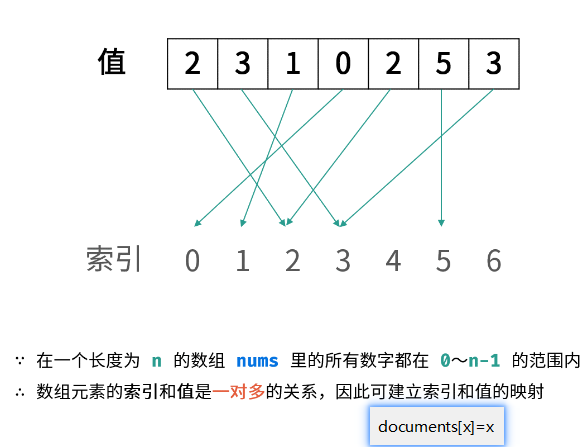
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
int N = nums.size();
for(int i=0; i<N; i++){
while(nums[i] != i){ //发现这个坑里的萝卜不是自己家的
int temp = nums[i]; //看看你是哪家的萝卜
if(nums[temp] == temp) //看看你家里有没有和你一样的萝卜
return temp; //发现你家里有了和你一样的萝卜,那你就多余了,上交国家
else //你家里那个萝卜和你不一样
swap(nums[temp], nums[i]); //把你送回你家去,然后把你家里的那个萝卜拿回来
}
}
return -1;
}
};
遍历数组,比较当前数组下标和当前数组上的值,如果相等,说明该元素有两个,不相等则把该元素放到它正确的位置上去
LCR 121. 寻找目标值 - 二维数组
思路1:使用两层循环暴力破解
暴力法未利用矩阵 “从上到下递增、从左到右递增” 的特点,显然不是最优解法。
思路2:“围城”
题目给的二维数组有个特点:每行首个元素一定是本行最小元素,我们可以利用这个特点来完成由底至上的查找。
将矩阵从右上角“拎”起来,并将其转化为图形式,发现其类似于二叉搜索树
左分支元素更小、右分支元素更大
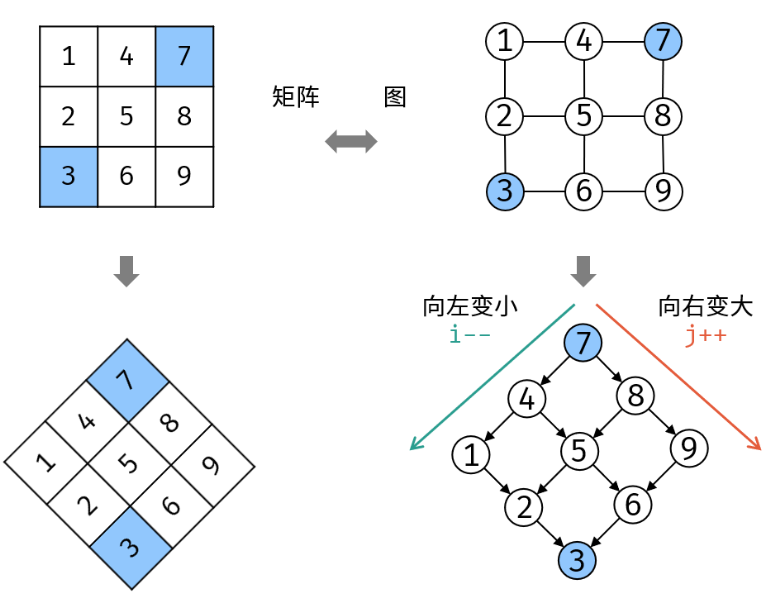


由此,时间复杂度由MN降低到了M+N;
154. 寻找旋转排序数组中的最小值 II
思路1:利用头尾比较
但好像没有做出来?

思路2:二分法
找最小值,即寻找旋转点的位置。

C情况解析:

实际上,当出现 nums[m]=nums[j]nums[m] = nums[j]nums[m]=nums[j] 时,一定有区间 [i,m][i, m][i,m] 内所有元素相等 或 区间 [m,j][m, j][m,j] 内所有元素相等(或两者皆满足)。对于寻找此类数组的最小值问题,可直接放弃二分查找,而使用线性查找替代。
343. 整数拆分
如何解决重复选择数字?
思路1:动态规划



思路2:数学规律
LCR 135. 报数
思路1:傻瓜式解法
思路2:字符串模拟
首先要考虑到当n很大的时候(比如100),打印出来的数很有可能是超过了INT_MAX的范围的,所以我们用字符串来表示每个数。
模拟思路:初始化字符串为“000...”,用它来循环模拟1到n位最大数。

char与int运算:

思路3:dfs模拟
辅助函数 dfs(x, len) 的作用是:生成长度为len的数字,正在确定第 x 位。当 x=0 时表示左边第一位,不能为0,这样可以避免出现 0 开头的字符串。
class Solution {
vector<string> res;
string cur;
char NUM[10] = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
// 生成长度为 len 的数字,正在确定第x位(从左往右)
void dfs(int x, int len) {
if(x == len) {
res.push_back(cur);
return;
}
int start = x==0? 1 : 0; // X=0表示左边第一位数字,不能为0
for(int i=start; i<10; i++) {
cur.push_back(NUM[i]); // 确定本位数字
dfs(x+1, len); // 确定下一位数字
cur.pop_back(); // 删除本位数字
}
}
public:
vector<string> printNumbers(int n) {
for(int i=1; i<=n; i++) // 数字长度:1~n
dfs(0, i);
return res;
}
};
LCR 139. 训练计划 I
思路1:双指针
原本思路:
if (actions[head]%2 ==0){
swap(actions[head],actions[tail]);}
这样做是错误的,原因在于,只在头指针遇到偶数时交换,会导致最后的数组并不是按照分部有序排列的。
注意:本题的双指针需要维护一个状态:首个元素。
也就是说在两方都找到各自的首个符合规则的元素并执行交换后,需要使状态回到未找到首个符合规则的元素的状态。
实现如下:
while(i < j && (actions[i] & 1) == 1) i++;
while(i < j && (actions[j] & 1) == 0) j--;
思路2:快慢指针
fast的作用是向前搜索奇数位置,low的作用是指向下一个奇数应当存放的位置
fast和low均初始化为0;
169. 多数元素
疑惑:率先统计出来的频次如何被后来的频次取代?
思路1:排序
众数在整个有序数组中的分布一定是居中的。
思路2:摩尔投票
此消彼长
当votes时,重置众数。


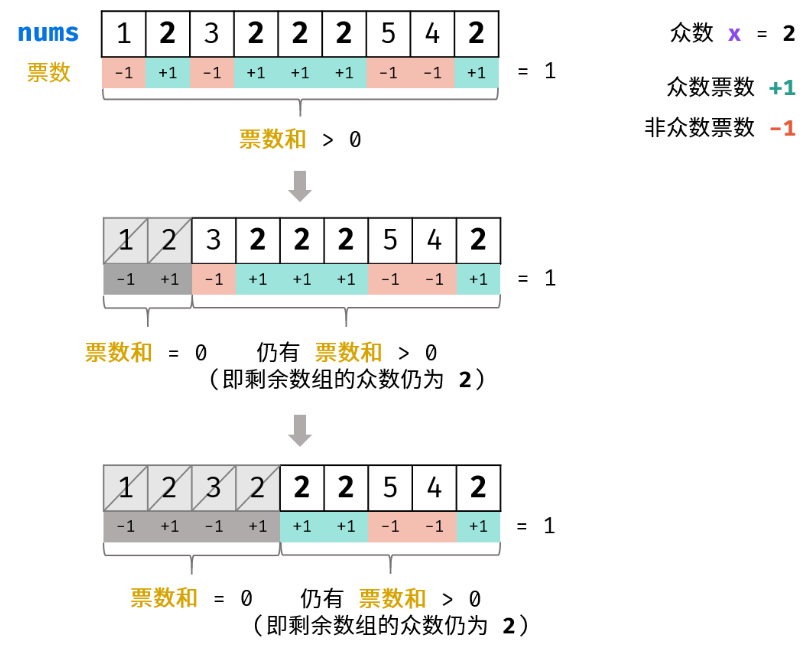
class Solution {
public:
int majorityElement(vector<int>& nums) {
int x = 0, votes = 0;
for (int num : nums){
if (votes == 0) x = num;//设置新选举对象
votes += num == x ? 1 : -1;//判断是否是当前选举对象?是则+1不是-1,直到票数扣减到0
}
return x;
}
};
思路3:哈希
class Solution {
public:
// 定义公共成员函数 majorityElement,接受一个整数向量引用作为参数
int majorityElement(vector<int>& nums) {
// 使用一个无序映射(unordered_map),key 为整数,value 为该整数在数组中出现的次数
unordered_map<int, int> mp;
// 遍历输入数组 nums
for (int n : nums) {
// 对于遍历到的每个整数 n,
// 先递增该整数在映射 mp 中对应的计数(如果不存在,则插入并初始化为 1)
++mp[n];
// 接下来判断当前整数 n 的出现次数是否已经超过数组大小的一半
// 如果超过,则说明找到了众数,直接返回这个整数
if (mp[n] > nums.size() / 2) {
return n;
}
}
// 如果遍历完整个数组都没有找到满足条件的众数,则返回一个特殊值 -1 表示没有这样的元素
return -1;
}
};
LCR 159. 库存管理 III
思路1:sort()
思路2:快速排序(代替无脑sort),参看后面排序板块笔记
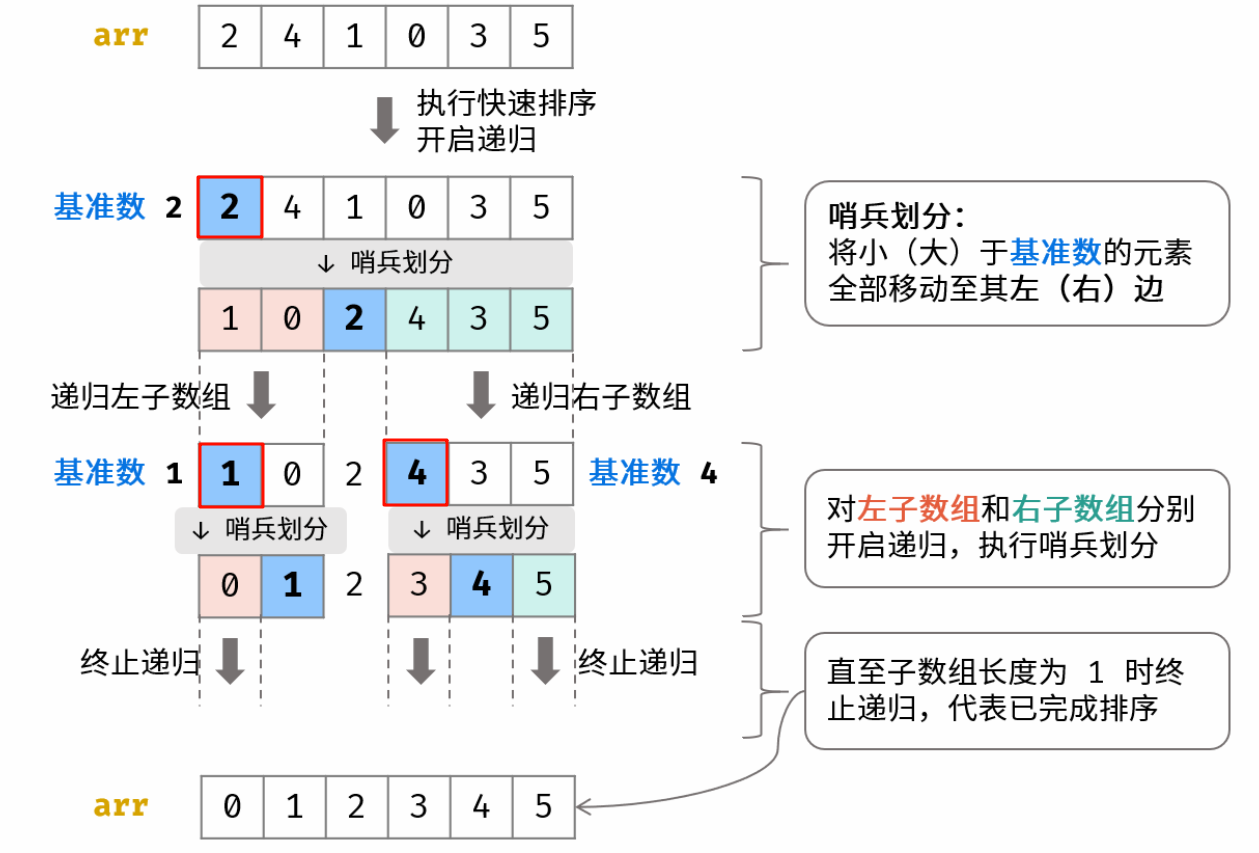
哨兵划分操作: 以数组某个元素(一般选取首元素)为 基准数 ,将所有小于基准数的元素移动至其左边,大于基准数的元素移动至其右边。
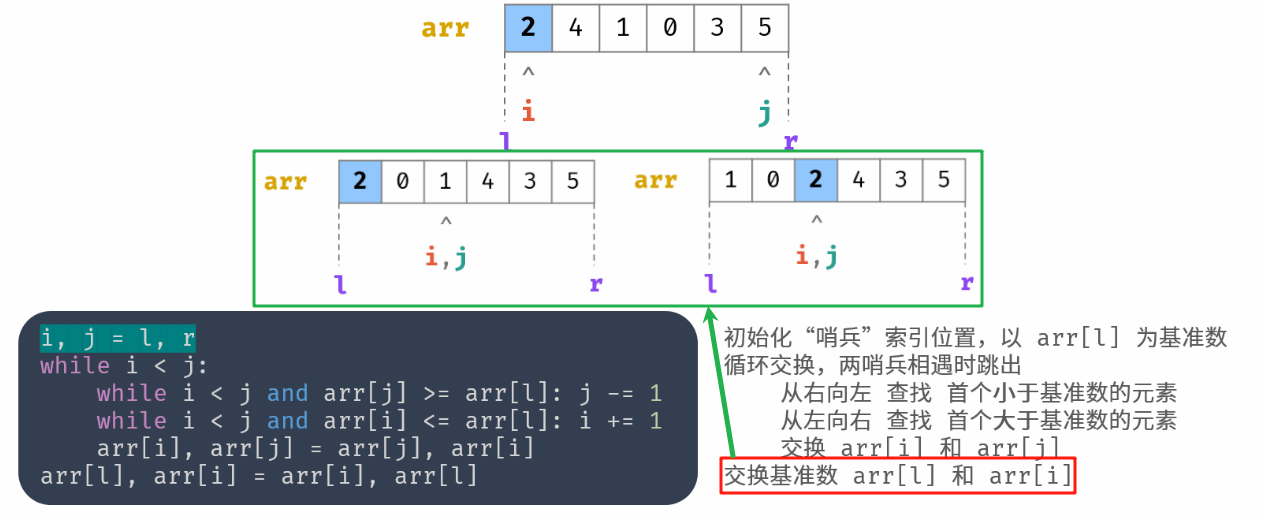
第一步完成。
递归: 对 左子数组 和 右子数组 递归执行 哨兵划分,直至子数组长度为 1 时终止递归,即可完成对整个数组的排序。
void quickSort(vector<int>& stock, int l, int r) {
// 子数组长度为 1 时终止递归
if (l >= r) return;
// 哨兵划分操作(以 stock[l] 作为基准数)
int i = l, j = r;
while (i < j) {
while (i < j && stock[j] >= stock[l]) j--;
while (i < j && stock[i] <= stock[l]) i++;
swap(stock[i], stock[j]);
}
swap(stock[i], stock[l]);
// 递归左(右)子数组执行哨兵划分
quickSort(stock, l, i - 1);
quickSort(stock, i + 1, r);
}

注意:递归执行快排函数时,传入对应界限要执行减一操作
思路3:快速选择
既然题目并不对返回数组的顺序做要求,那么我们其实只需要找出一个大小的分界点即可。
根据快速排序原理,如果某次哨兵划分后 基准数正好是第 cnt+1小的数字 ,那么此时基准数左边的所有数字便是题目所求的 最小的 cnt 个数 。

vector<int> quickSort(vector<int>& stock, int cnt, int l, int r) {
int i = l, j = r;
while (i < j) {
while (i < j && stock[j] >= stock[l]) j--;
while (i < j && stock[i] <= stock[l]) i++;
swap(stock[i], stock[j]);
}
swap(stock[i], stock[l]);
if (i > cnt) return quickSort(stock, cnt, l, i - 1);
if (i < cnt) return quickSort(stock, cnt, i + 1, r);
vector<int> res;
res.assign(stock.begin(), stock.begin() + cnt);
return res;
}
注意:
while判断中的是<=和>=符号。
assign函数: 将一个容器中元素全部复制到另一个容器中:
void assign(const_iterator first,const_iterator last); void assign(size_type n,const T& x = T());
295. 数据流的中位数
思路:对顶堆
将所有比中位数小的数值存在small堆中,比中位数大的数值存在big堆中,并且保证两堆容量之差小于等于1。这样,中位数就一定在两个堆的堆顶之中。我们将这种堆称为对顶堆。
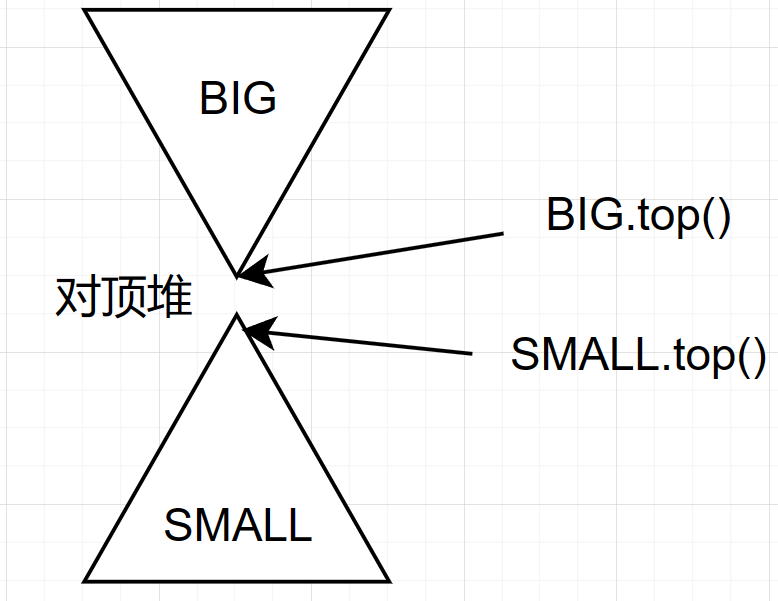
小、大顶堆定义:
// 初始化小顶堆
priority_queue<int, vector<int>, greater<int>> minHeap;
// 初始化大顶堆
priority_queue<int, vector<int>, less<int>> maxHeap;
堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看,我们可以将“优先队列”和“堆”看作等价的数据结构。
其中,大顶堆的定义是在小顶堆的基础上实现的,加上了优先级。
插入数据操作:
- 若小顶堆为空,优先添加到小顶堆中(初始操作)
- 若接下来要添加的数字小于小顶堆的TOP,则添加到小顶堆中;反之大顶堆
插入数据后要实时维护两堆状态,若小顶堆的元素数量超过大顶堆元素数量为2,则从小顶堆中取出元素;反之亦然。

优化: 更好的插入方法,从思想上减少繁杂的插入逻辑判断: 由于不能判断即将插入的数字到底应该存放在哪个堆中,故应该先将元素插入大顶堆中,如果此元素大于了原本大顶堆的元素,在插入后,自然会回到堆顶来,此时加入小顶堆并弹出即可。若此元素本就属于大顶堆,为了平衡元素数量,也对大顶堆的堆顶元素换位。
- m=n:A添加一个元素。实现方法:将新元素num插入至B,再将 B 堆顶元素插入至 A
- m≠n:B添加一个元素。实现方法:将新元素num插入至A,再将 A 堆顶元素插入至 B
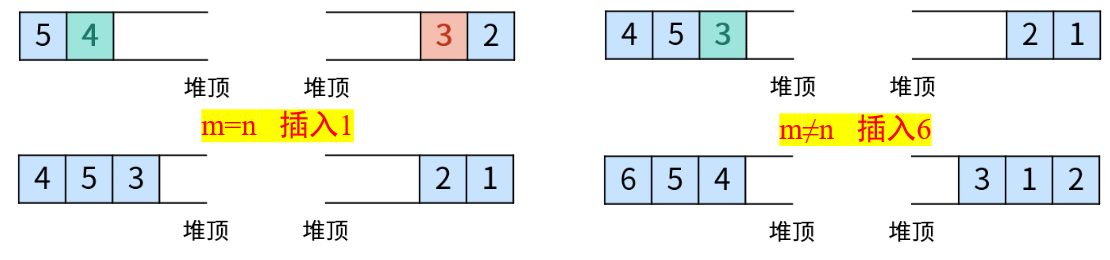
m=n时,为什么选择往大顶堆里面放?如果选择往小顶堆放,如果插入的数本来就属于小顶堆,那正好;如果插入的数字本来属于大顶堆,插入后打破了大小规则。
记住:始终维护小顶堆≥大顶堆元素数量(便于返回中位数)
LCR 164. 破解闯关密码
思路1:内置sort函数
首先要将题目给出的排序规则转换为程序语言。
拼接字符串,若:
- x+y>y+x:x>y
- x+y<y+x:x<y
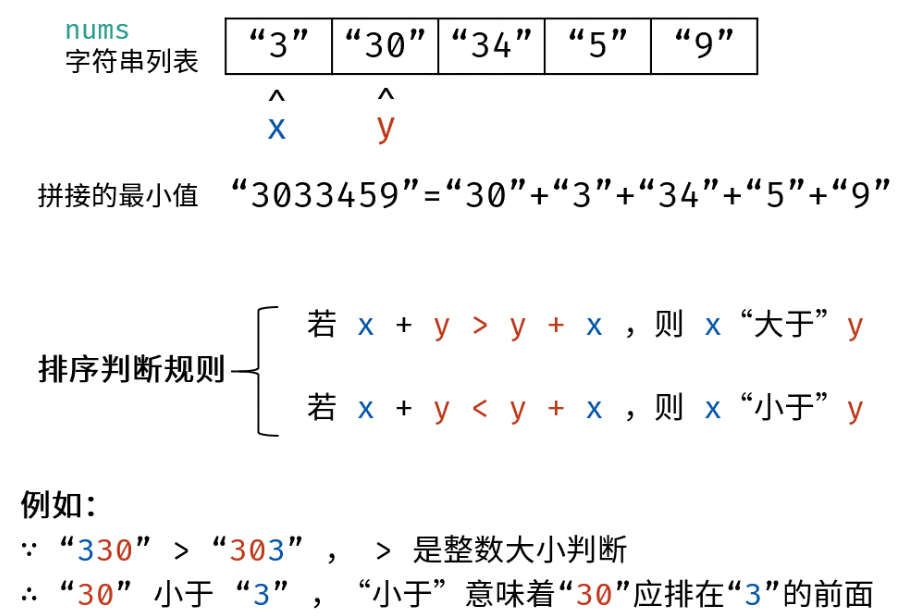
sort(strs.begin(), strs.end(), [](string& x, string& y){ return x + y < y + x; });
思路2:快速排序
思路和之前的题目一致,都是为了达到sort()函数的效果。
这里贴出比较方式:
while(strs[j] + strs[l] >= strs[l] + strs[j] && i < j) j--;
while(strs[i] + strs[l] <= strs[l] + strs[i] && i < j) i++;
264. 丑数 II
首先要解析何为丑数?
- 1 是最小的丑数。
- 对于任意一个丑数 x,其与任意的质因数(2、3、5)相乘,结果(2x、3x、5x)仍为丑数。
思路1:小顶堆
- 首先将最小丑数入列;
- 每次取出堆顶元素,对堆顶元素进行X2、X3、X5操作,入队;
为了防止同一丑数多次入队,利用Set去重
去重逻辑:
set<long> s;
s.count(t);//每次往堆内添加元素前,先利用count函数检查堆内是否有此数
思路2:动态规划(三指针)
不难发现,所谓丑数,后面的丑数的产生是对前面的丑数有依赖性的:
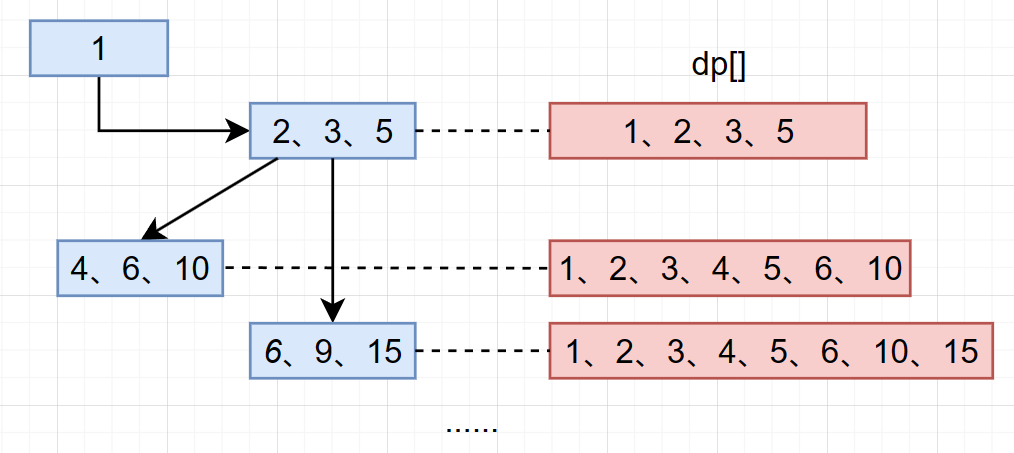
dp[i]=min(dp[i2]*2,dp[i3]*3,dp[i5]*5)
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> res(1,1);
int i2=0,i3=0,i5=0,i=1;
while(i++<n){
int tmp=min(2*res[i2],min(3*res[i3],5*res[i5]));
res.push_back(tmp);
if(tmp==2*res[i2]) i2++;
if(tmp==3*res[i3]) i3++;
if(tmp==5*res[i5]) i5++;
}
return res.back();
}
};
小顶堆的方法是先存(一个乘数出来,存入三个结果)再排,dp的方法则是先排再存(其中一个)
LCR 170. 交易逆序对的总数
注意题意:前一天的股价高于后一天的股价是指前一天的股价比后面某一天的股价高,不是特指相邻天。
思路:归并排序
由于题目中给的数组大小范围是:0~50000,所以我们需要将原数组拆分后,来解决问题。
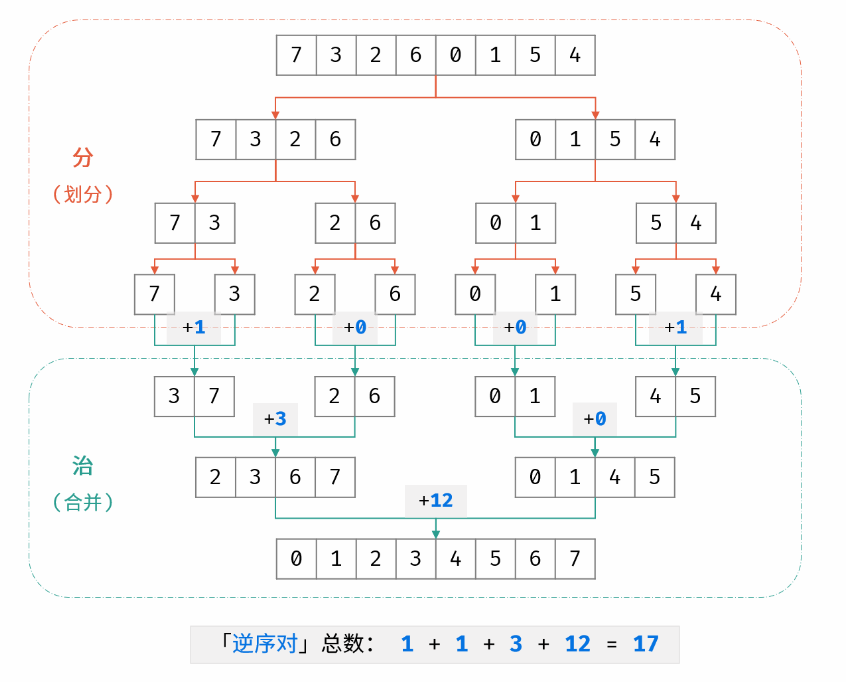
划分:

int m = (l + r) / 2;
int res = mergeSort(l, m, record, tmp) + mergeSort(m + 1, r, record, tmp);
合并:
- 创建临时数组,大小:right-left+1
- 创建两指针,分别指向左右数组首元素(注意:此时数组元素是乱序的)
- 当两个数组都有元素时,遍历比较每个元素大小
- 比较两个数组的元素,取较小的元素加入到临时数组中。并将两个指针指向下一个元素
- 当左边数组元素大于右边数组元素时,即产生了逆序对。统计左边元素及其后元素个数
- 当某一侧数组遍历完成后,执行保底操作:将另侧数组元素加入临时数组。此时,临时数组是有序的
vector<int> tmp(right - left + 1);
// 初始化左子数组和右子数组的起始索引
int i = left, j = mid + 1, k = 0;
int cnt=0;
// 当左右子数组都还有元素时,进行比较并将较小的元素复制到临时数组中
while (i <= mid && j <= right) {
if (nums[i] <= nums[j])
tmp[k++] = nums[i++];
else
tmp[k++] = nums[j++];
cnt++;//
}
// 将左子数组和右子数组的剩余元素复制到临时数组中
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
for (k = 0; k < tmp.size(); k++) {
nums[left + k] = tmp[k];
}
关注:何时元素变得有序? 在上图中,关注37-26->2367的过程。
在检测到3>2后,逆序对统计+2.2被加入临时数组。//j++
随后3又被拿来和6比较,3<6,3被加入临时数组。//i++
随后轮到7...
34. 在排序数组中查找元素的第一个和最后一个位置
题目要求时间复杂度为:对数阶,所以此题必须使用二分查找
思路:二分查找
二分查找可以理解为红蓝区域不断扩大的问题,而二分与朴素算法的差异是二分扩展的步长每次都是一半,朴素算法每次扩展一位。
二分查找法模板
//l=0,r=size()-1
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = (l + r)/2;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
//
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = ( l + r + 1 ) /2;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
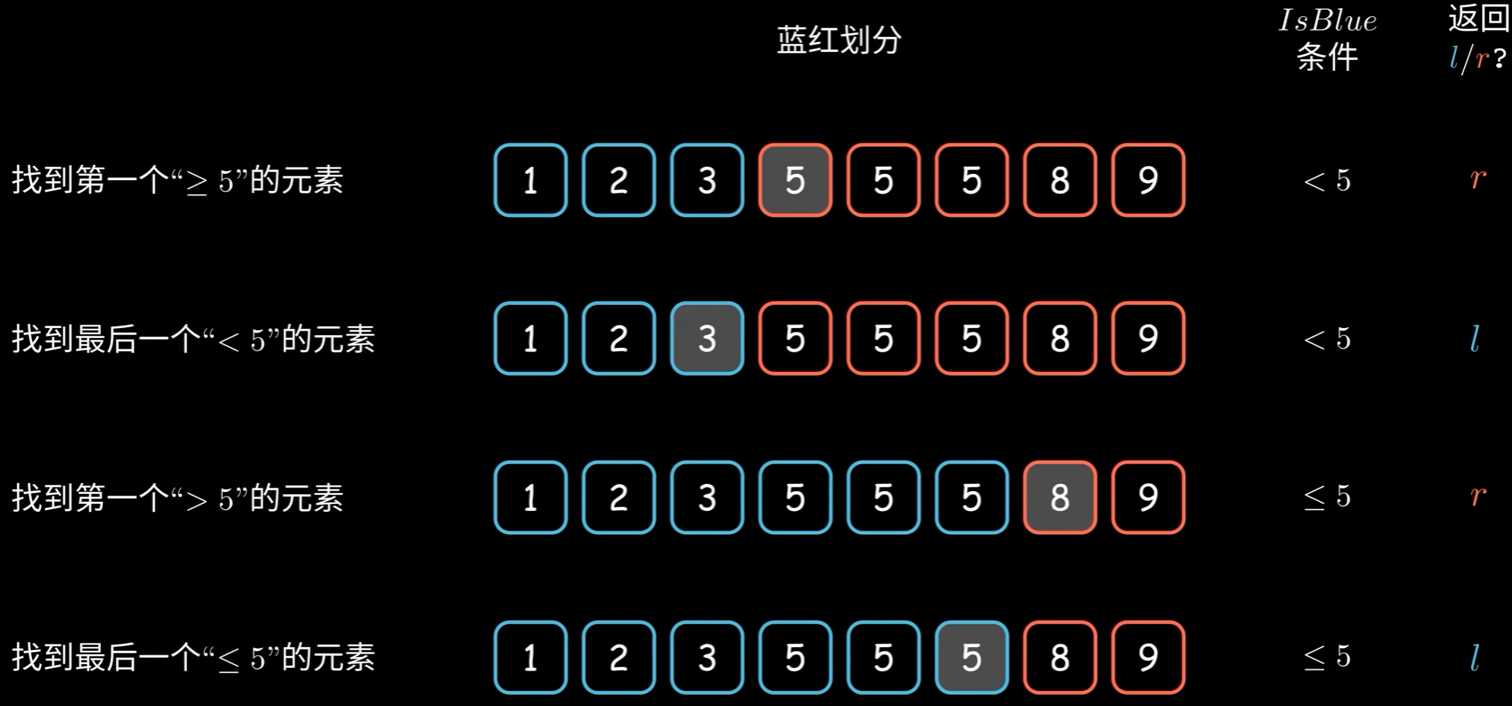
1,3情况在CPP中有对应库函数:std::lower_bound()、std::upper_bound()
使用二分分别查找出第一个大于和小于目标元素的元素的位置
LCR 173. 点名
思路:二分查找
排序数组中的搜索问题,首先想到 二分法 解决。
数组的划分条件是,当nums[i]==i时,说明左端数组对应正常。应该移动左指针到m+1处。
初始化:l=0,r=size()-1
LCR 179. 查找总价格为目标值的两个商品
思路:双指针
注意题目中的升序数组这一条件,所以我们选择将双指针的两指针初始化在数组两端。
双指针思路正确性证明:
假想如下矩阵存在:
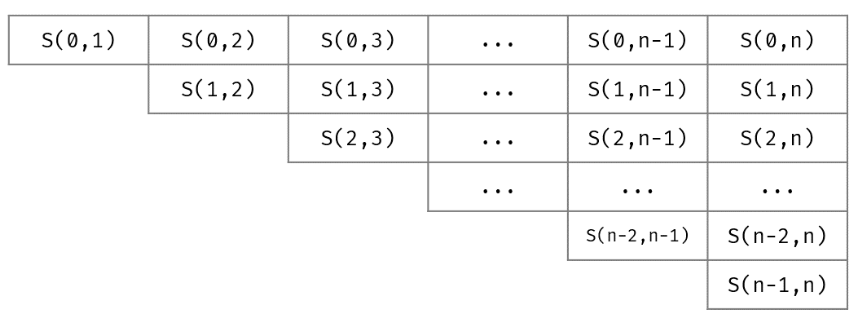
当我们由S(I,J)切换到S(I+1,J)时,相当于是直接忽略了一行元素,为什么这样操作是安全的呢?当上一行最后一个状态都无法满足S>target的情况时,上一行的前面的元素自然也无法满足,故可安全略去。
思路2:哈希
主要还是利用的哈希的去重性质。
class Solution {
public:
unordered_set<int> ss;
vector<int> twoSum(vector<int>& nums, int target) {
for (int i = 0; i < nums.size(); i++) {
int find = target - nums[i];
if (find < 0) return vector<int>();
if (ss.count(find) != 0) return vector<int>{nums[i], find};
ss.insert(nums[i]);
}
return vector<int>();
}
};
先将nums[i]加入数组,相当于把另一个目标数提前加入哈希表,若遍历到目标数,count()函数会返回-1,即找到数对。
思路3:二分查找
依次设定左值,右侧的数采用二分查找
LCR 180. 文件组合
思路:滑动窗口
原本思路错误点:
- 没必要遍历全员,到了某一阈值后,后续所有值均无效
- 窗口到底多大?不用管,该多大多大
- 不等于目标值时,不能一概而论,需要根据大小关系决定移动哪侧指针
当s=target时:记录连续整数序列,并向右移动左边界i=i+1;
当s>target时:向右移动左边界i=i+1,并更新元素和s;
当s<target时:向右移动左边界j=j+1,并更新元素和s;
这样设计的巧妙之处在于,=和>的逻辑可以合二为一,由于=情况后也需要向后移动左侧指针,寻找下一组答案。
239. 滑动窗口最大值
如何去维护窗口内数据的最大值?
思路:单调队列(deque)
本题难点: 如何在每次窗口滑动后,将 “获取窗口内最大值” 的时间复杂度从 O(k)降低至 O(1)


class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
if(nums.size() == 0 || k == 0) return {};
deque<int> deque;
vector<int> res(nums.size() - k + 1);
for(int j = 0, i = 1 - k; j < nums.size(); i++, j++) {//j是窗口左侧,i是窗口右侧
if(i > 0 && deque.front() == nums[i - 1])//窗口装满了,从队列中删除元素
deque.pop_front();
// 保持 deque 递减
while(!deque.empty() && deque.back() < nums[j])
deque.pop_back();//当插入元素大于队头元素时,清空队列中所有元素
deque.push_back(nums[j]);
// 记录窗口最大值
if(i >= 0)
res[i] = deque.front();
}
return res;
}
}
};
LCR 186. 文物朝代判断
理解题意:是否能利用数组中的0,将0变为1~13的任意数字,使得该数组连续

思路1:哈希表辅助去重
遍历数组,遇0跳过。
不断更新max与min。后续思路与思路二一致。
利用set去重。
思路2:排序
先对数组执行排序。接着统计0数量,0右侧首数字即为最小者,遍历结束指针所指即为最大者。将两者值相减,若相差小于数组大小(5)则认为满足连续条件。
LCR 189. 设计机械累加器
思路1:逻辑运算符短路效应
if(A && B) // 若 A 为 false ,则 B 的判断不会执行(即短路),直接判定 A && B 为 false
if(A || B) // 若 A 为 true ,则 B 的判断不会执行(即短路),直接判定 A || B 为 true
题目的难点是无法使用if等判断符,所以这里我们考虑使用&&来执行判断。
在&&两侧的条件中,两侧条件均为真,整个表达式取值才为真。但若&&左侧表达式为假,无论右侧表达式的取值如何,整个表达式的取值均假。
利用这个特性,我们将target由原本逐渐减小为1,当<1时退出累加逻辑。
target > 1 && (target += mechanicalAccumulator(target - 1));
思路2:二维数组+右移运算符
太秀了~
我们考虑到要对1~target的整数求和,由于其数学特性,S=(1+target)*target/2.我们可以使用二维数组来模拟此过程,声明二维数组target,target+1,求此数组的大小即可求得此等差数列的值。
return sizeof(bool[target][target+1])>>1;
注意,此处采用的是bool类型(char)的数组,意在减少内存空间的占用。
LCR 191. 按规则计算统计结果
题目的隐藏指示:不能使用除法,因为测试样例中含有0.这也使得我们不得不放弃使用暴力解法。
思路1:动态规划(前缀和?)
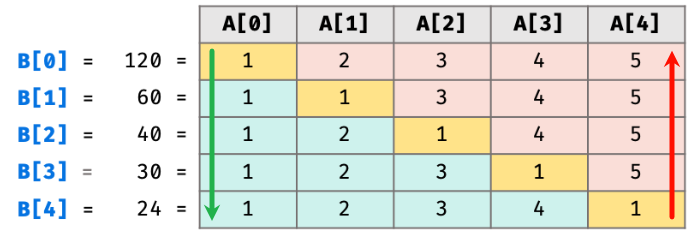
for(int i = 1; i < len; i++) {
arrayB[i] = arrayB[i - 1] * arrayA[i - 1];//累计乘
}
for(int i = len - 2; i >= 0; i--) {
tmp *= arrayA[i + 1];//累计乘
arrayB[i] *= tmp;
}
前缀和科普:
一维前缀和是指:

二位前缀和是指:

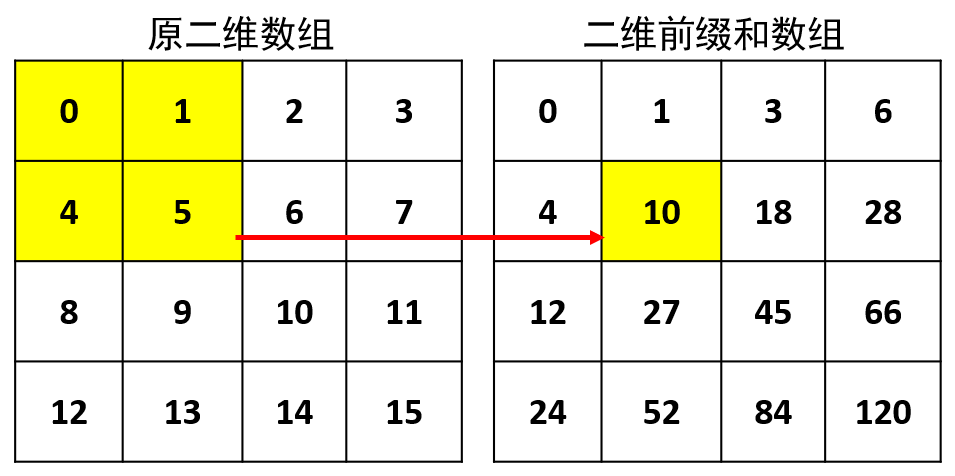
前缀和是一种预处理,用于降低查询时的时间复杂度。
例如:给定n个整数,进行m次询问,每次询问返回区间内值的和。
我们在处理数组时,可以预先计算前缀和数组
字符串
LCR 122. 路径加密
思路1:新建字符串
遍历两字符串,适时替换字符。
思路2:扩容原地交换
题目条件更改为:将原字符串中的“.”替换为“%20”,原字符串中可能不止存在一处空格
统计原字符串中“.”的数量,将字符串转换为数组后,扩容为(原数组长度+数量*2)
初始化双指针如下图:
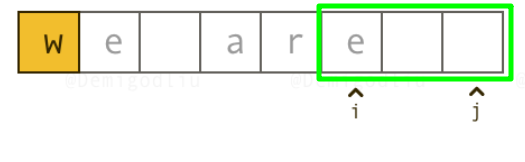
这样初始化的目的是为将来替换数组内容做准备,将J置于新数组的末尾,一旦I指向的数据不为空,则交换位置,将非空数据后移;当I指向空时,即刻执行替换,I不动,J向前逐位替换,直到向前移动2位为止。
LCR 157. 套餐内商品的排列顺序
思路:回溯
题目里面没有说所提供的字符串不包含重复字符
关于回溯中去重的方案有两种:
- 利用set去重
- 额外增加标志位去重
问题:
- 三个数组声明于何处?used、path声明在共有域,res声明在私有域(或res+path声明在私有域,used声明在公有域)
- 剪枝操作:当当前元素与前一元素值相同且used[i-1]为false时执行剪枝
if(i>0 && goods[i]==goods[i-1] && !used[i-1]){continue;}
used[i - 1] == true,说明同一树支nums[i - 1]使用过 used[i - 1] == false,说明同一树层nums[i - 1]使用过
设置固定位,也就是当前选中加入结果的字符串位,回溯前交换下一位和回溯位,回溯后交换回来
for(int i=x;i<goods.size();i++){
if(st.find(goods[i] != st.end())){
continue;
}
st.insert(goods[i]);
swap(goods[i],goods[x]);
dfs(goods,x+1);
swap(goods[i],goods[x]);
}
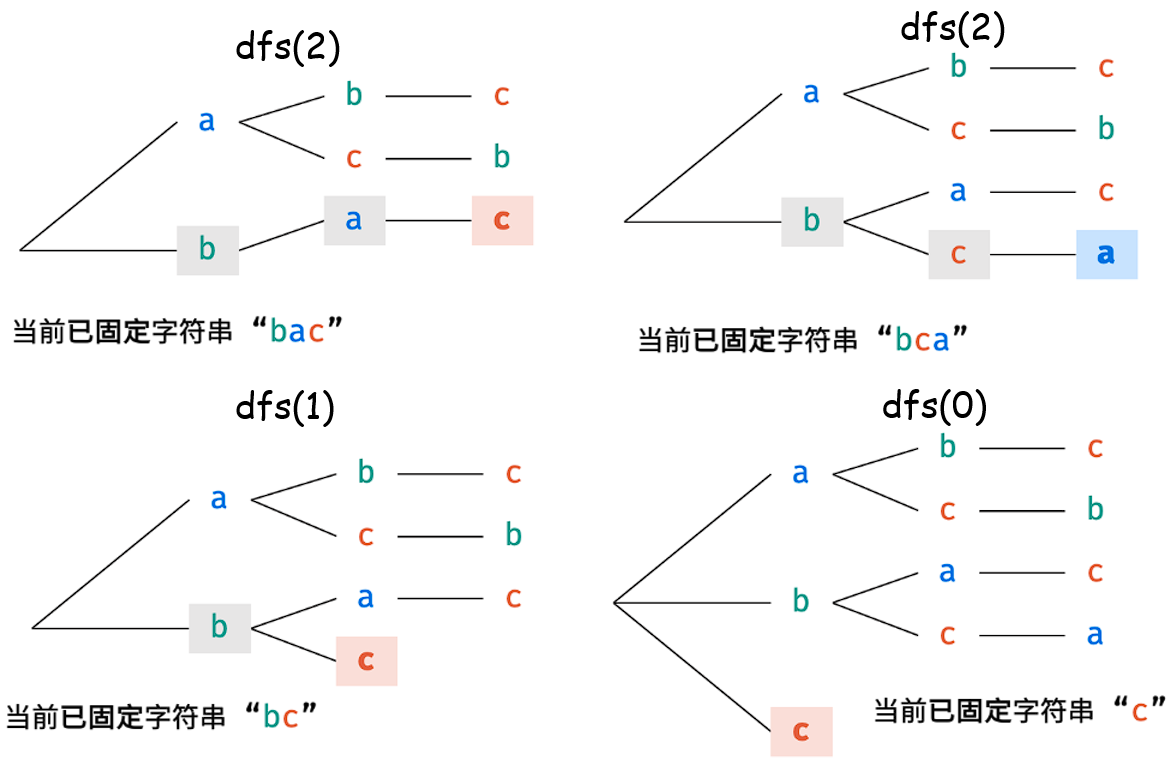
利用固定位X和交换操作达成去重操作
LCR 138. 有效数字
思路:有限状态自动机
将有效数字的构成转换为自动机的状态。
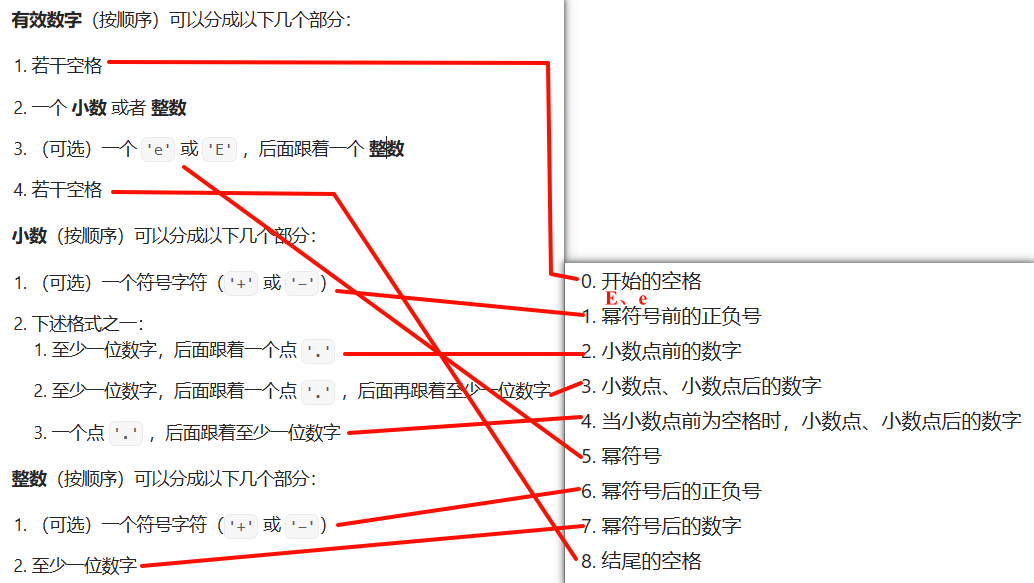
各个状态之间是可以转移的,我们将本状态能转换到的状态利用典型的key-value结构存储,使用HashMap。
如何执行转换呢?

而当字符类型不在哈希表中时,状态转换终止。
利用最终状态与合法的最终状态比较。(2、3、7、8)
3. 无重复字符的最长子串
思路1:滑动窗口
初始化双指针a、b,均指向数组首位。
b向右移动,对于每个A[b],判断是否在之前的数组中出现过,若出现过,则将a移至复现位置右侧。
注意C++中哈希表的使用
for(int j=0;j<len;j++){
if(dic.find(s[j])!=dic.end()){
i=max(i,dic.find(s[j])->second);
}
dic[s[j]]=j;
res=max(res,j-i);
思路2:Hashmap优化
仅当s[start,end) 中存在s[end]时更新start
if (hash.find(tmpChar) != hash.end() && hash[tmpChar] >= start)
{
start = hash[tmpChar] + 1;
length = end - start;
}
思路3:桶优化
vector<int> vec(128, -1);//利用桶代替HashMap
/*
利用26位表示全部字母(大+小写)
128位用于ASCII码
出现则将原初始化的值由-1->出现之后的位置
*/
仅当s[start,end) 中存在s[end]时更新start
if (vec[int(tmpChar)] >= start)
{
start = vec[int(tmpChar)] + 1;
length = end - start;
}
LCR 169. 招式拆解 II
思路1:普通哈希表
遍历字符串,使用哈希表统计各字符的数量(若存在该字符,则将value置为false;若不存在,则添加并置true)
遍历字符串,返回首个数量为一的字符(哈希表查找时间复杂度为1)
思路2:有序哈希表
在思路1的基础上,针对第二次遍历字符串做优化,采用有序哈希表(键值对的插入是按顺序的)
由于 C++ 未提供自带的链式哈希表,因此借助一个 vector 按序存储哈希表 hmap 中的 key ,第二轮遍历此 vector 即可。
实现细节:
vector<char> keys;
unordered_map<char, bool> hmap;
if(hmap.find(c)==hamp.end())
keys.push_back(c);//后续比较value值的时候,不需要像方法1一样重新遍历整个字符串
hmap[c]=(hamp.find(c)==hmap.end());
最后一句的意思是,如果存在C的话,find()返回的C的指针不应为空(hamp.end()),则将C对应位置value置为true;若再次遇到C,后面表达式的值应该为false.
哈希表理论基础复习
快速判断一个元素是否出现在集合内
常见的哈希结构:
- 数组
- map
- set
集合 底层实现 是否有序 数值是否可以重复 能否更改数值 查询效率 增删效率 std::set 红黑树 有序 否 否 O(log n) O(log n) std::unordered_set 哈希表 无序 否 否 O(1) O(1)
映射 底层实现 是否有序 数值是否可以重复 能否更改数值 查询效率 增删效率 std::map 红黑树 key有序 key不可重复 key不可修改 O(logn) O(logn) std::unordered_map 哈希表 key无序 key不可重复 key不可修改 O(1) O(1)
151. 反转字符串中的单词
思路1:双指针
既然是要反转字符串,那就使用双指针从原字符串末尾往前遍历,添加的逻辑是从i~j,不存在字符串内部乱序可能。
- 去除字符串两侧空格(Java使用.trim())
- 搜索首个空格
- 添加单词
- 跳过单词间空格
void removeExtraSpaces(string& s) {
int slowIndex = 0, fastIndex = 0; // 定义快指针,慢指针
// 去掉字符串前面的空格
while (s.size() > 0 && fastIndex < s.size() && s[fastIndex] == ' ') {
fastIndex++;
}
for (; fastIndex < s.size(); fastIndex++) {
// 去掉字符串中间部分的冗余空格
if (fastIndex - 1 > 0
&& s[fastIndex - 1] == s[fastIndex]
&& s[fastIndex] == ' ') {
continue;
} else {
s[slowIndex++] = s[fastIndex];
}
}
if (slowIndex - 1 > 0 && s[slowIndex - 1] == ' ') { // 去掉字符串末尾的空格
s.resize(slowIndex - 1);
} else {
s.resize(slowIndex); // 重新设置字符串大小
}
}
//主函数
string reverseWords(string s) {
removeExtraSpaces(s);
reverse(s, 0, s.size() - 1);
for(int i = 0; i < s.size(); i++) {
int j = i;
// 查找单词间的空格,翻转单词
while(j < s.size() && s[j] != ' ') j++;
reverse(s, i, j - 1);
i = j;
}
return s;
}
思路2:利用栈实现
将整个单词作为整体入栈
注意出栈时,先stack.top()再stack.pop(),并拼接空格
LCR 182. 动态口令
思路1:字符串切片
CPP:substr();
JAVA:substring();
思路2:遍历拼接(思路1不被允许的情况)
先向临时字符串添加t~size-1的字符,再添加余下字符
求余运算优化:
res.append(password.charAt(i % password.length()));//i初始值为target
8. 字符串转换整数 (atoi)
字符串转数字:

越界处理:

if (res > bndry || res == bndry && c[j] > '7') return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
或使用Long型保存结果:
long res = 0;
if (res >= INT_MAX && flag == 1) return INT_MAX;
if (res > INT_MAX && flag == -1) return INT_MIN;
补充:28. 找出字符串中第一个匹配项的下标
KMP算法:解决字符串匹配问题
前缀:包含首字母不包含尾字母的所有字串
后缀:包含尾字母不包含首字母的所有字串
最长相等前后缀:
模式串aabaaf前缀表为:
| a | aa | aab | aaba | aabaa | aabaaf |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 2 | 0 |
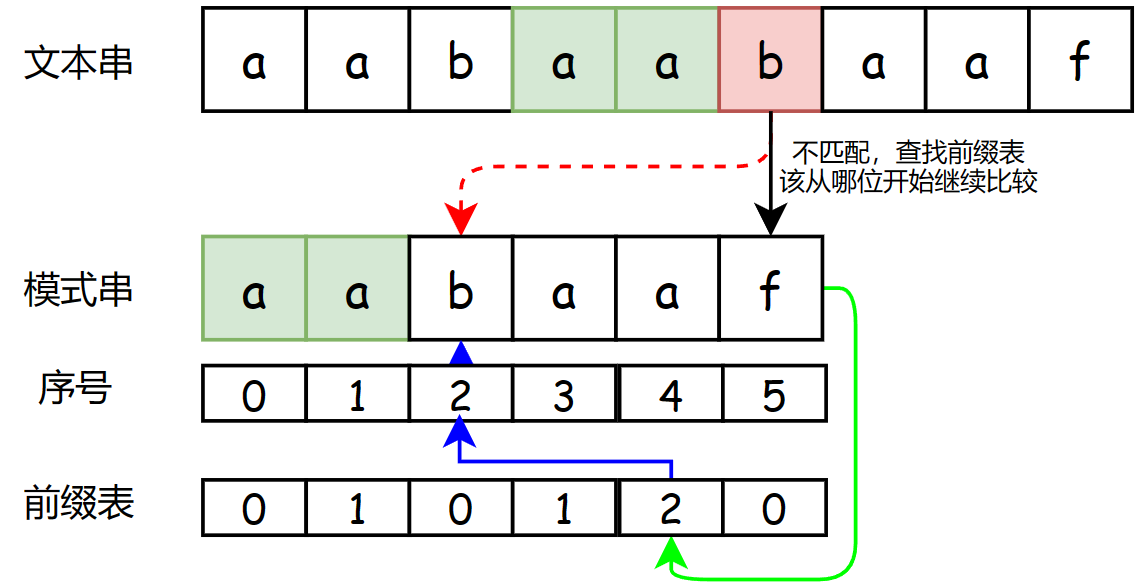
求前缀表(next数组):
初始化:初始化两个指针,i代表后缀末尾,j代表前缀末尾。
int i,j=0;
next[0]=0;
前后缀不相同的情况:当前后缀不相同时,我们要把前缀指针(j)回退到相等的位置,回退流程借next数组实现
前后缀相同的情况:前后缀相同时,更新next数组
for(i=1;i<s.size();i++){
while(j>0 && s[i] != s[j]){
j=next[j-1];
}
if(s[i] == s[j]){
j++;
}
next[i]=j;
}
如何遍历文本串?
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
j = next[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == needle.size() ) {
return (i - needle.size() + 1);
}
}
链表
剑指offer06.从尾到头打印链表
思路1:递推+回溯
先递推到链表尾部,再回溯至链表头
void recur(ListNode* head) {
if(head == nullptr) return;
recur(head->next);
res.push_back(head->val);
}
思路2:辅助栈
利用栈的特点,配合链表从前向后访问,即可实现倒序输出
LCR 136. 删除链表的节点
思路1:双指针
这里使用双指针的目的是维护传入头结点的状态。
声明pre指针指向原头结点,cur指向pre的next域。
cur做值探测,pre做状态保留。
思路2:优化1
在头结点前先创建新头结点,这样不用判断是否为头结点
思路3:递归
为什么要用递归?其实也是对状态的维护。遍历整个链表,当遍历到链表末尾时结束。删除结点的操作在这个过程中一并解决。整个过程中没有修改头结点的状态。只修改了head的next域
ListNode* backTracking (ListNode* head, int val){
if (head == NULL ){
return head;
}
if(head->val == val){
return head->next;
}
head->next=backTracking(head->next,val);
return head;
}
删除链表倒数第N个结点
思路1:双指针
先将前指针提前移动cnt位,然后将两指针同步前移,直至前指针移至空(末尾元素后一位)。为什么要移到后一位呢?因为若是将pre移至链表末尾,那么返回的cur将指向cnt+1的位置。
思路2:辅助栈
206. 反转链表
思路1:外部容器
利用外部容器,将原链表中元素按序加入,反转顺序后,再依次修改原链表的值。
思路2:双指针迭代
声明两指针,初始化为head和head前的空间。
cur每次向前迭代,反转两指针之间的指针方向。
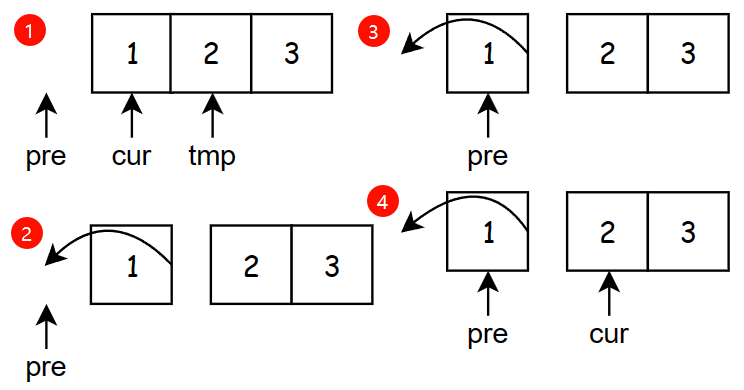
注意:要使用额外tmp变量存储cur后续结点,否则状态丢失。
末尾结点处理:
while(cru != nullptr)
思路3:递归
由于要返回的是反转后的链表,所以我们要在递归过程中维护一个变量,使其指向链表末尾元素。
递归的基本思路是,当前head元素指向head的前驱,前驱的next指针断掉。
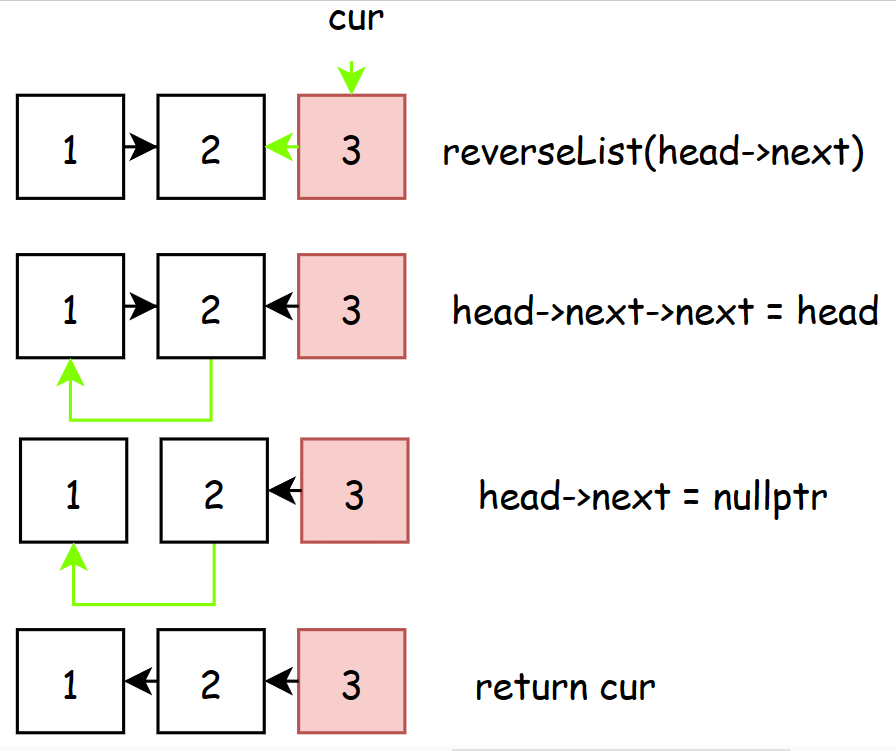
递归解题首先要做的是明确递推公式的含义,在这里对于结点1来说,它只需要知道它之后的所有节点反转之后的结果就可以了(不管具体怎么实现),也就是说递推公式reverseList的含义是:把拿到的链表进行反转,然后返回新的头结点。
ListNode* reverseList(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
ListNode* cur = reverseList(head->next);
head->next->next = head;
head->next = nullptr;
return cur;
}
拓展:翻转链表的部分
思路1:递归
基本思路可以参考上题解法三
先来看看反转1~N位的解法:
ListNode successor = null; // 后驱节点 ListNode reverseN(ListNode head, int n) { if (n == 1) { successor = head.next; return head; } ListNode last = reverseN(head.next, n - 1); head.next.next = head; head.next = successor; return last; }而对于本题,将递归的思想利用到极致,既然左侧端点可能不是最左侧的结点,那我们就利用递归逐步将区间[m,n]推至最左侧。
ListNode reverseBetween(ListNode head, int m, int n) { // base case if (m == 1) { return reverseN(head, n); } // 前进到反转的起点触发 base case head.next = reverseBetween(head.next, m - 1, n - 1); return head; }思路2:双指针
初始化两个指针,一个指向要翻转的首个结点的前面,一个指向首个翻转结点
首先将后面的指针的next断掉,单独保存
将断掉的单个结点接到前一个指针的next域
注意:本解法中两指针本身位置均未改变!!
21. 合并两个有序链表
思路1:快慢指针
忘记考虑初始结点的问题,两个头结点谁做初始结点不便于判断,故设虚拟头节点dum解决。并使cur指向dum,作为合并后链表上的指针。
另外,容易忽略的是,两链表长度并不相同,这点需要在代码中有所体现。
- 当L1值小于L2值时,cur的后继指定为L1,L1向前走一步
- 当L1值大于(等于)L2值时,cur的后继指定为L2,L2向前走一步
- 结点cur向前走一步
- 当L1或L2为空时,将剩余链表结点接在cur后
- 返回dum->next
思路2:递归
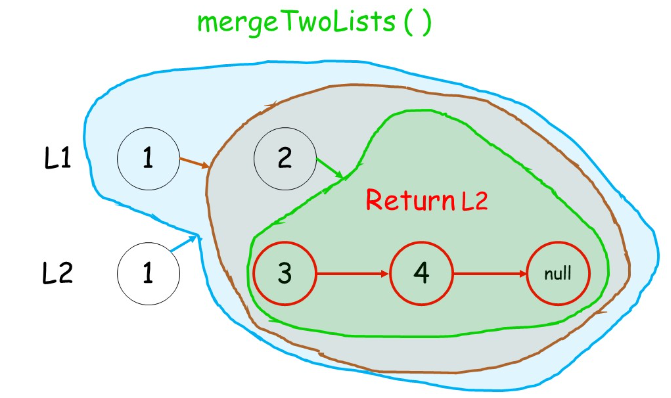
递归思想就是不管后面的操作如何,只管拿到结果返回
if (l1 == NULL) {return l2;}
if (l2 == NULL) {return l1;}
if(list1->val <= list2->val){
list1->next=mergeTwoLists(list1->next,list2);
return list1;
}
list2->next=mergeTwoLists(list2->next,list1);
return list2;
138. 随机链表的复制
本题难点:在复制链表的过程中构建新链表各节点的random引用指向。
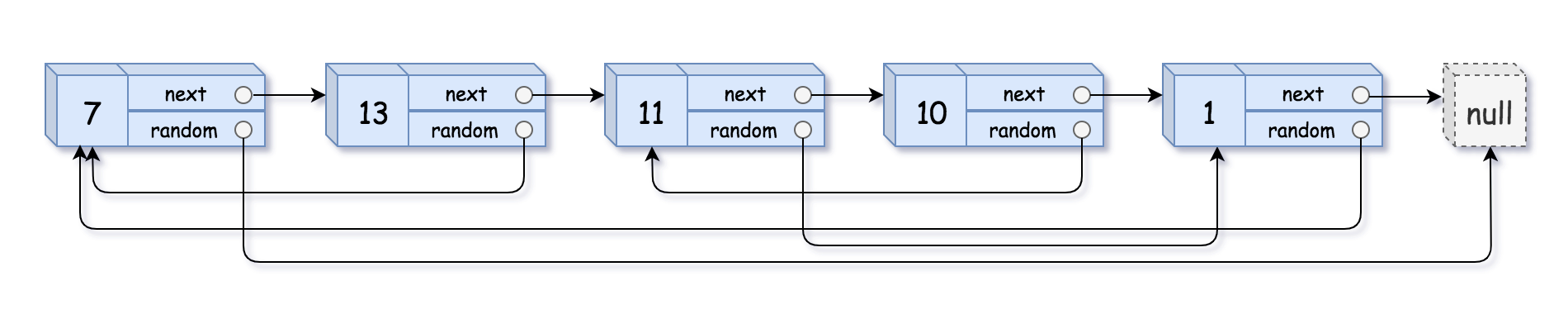
思路1:哈希表
由于结点需要维护的状态多了一个random指针,我们考虑利用哈希表结构构建原链表结点->新链表对应结点的关系
cur指针始终是在原链表上移动的,在创建random和next关系时,便于读取原链表中的关系。
map[cur]->next = map[cur->next];
map[cur]->random = map[cur->random];
为什么要使用哈希表来维护此关系呢?哈希表为我们提供了一个O(1)的查询,便于我们查找random和next结点。
思路2:拼接+拆分
利用原链表的关系,在原链表中加入新链表节点,在访问原链表结点的random和next关系时,访问新链表元素的random和next。

class Solution {
public:
Node* copyRandomList(Node* head) {
if(head == nullptr) return nullptr;
Node* cur = head;
// 1. 复制各节点,并构建拼接链表
while(cur != nullptr) {
Node* tmp = new Node(cur->val);
tmp->next = cur->next;
cur->next = tmp;
cur = tmp->next;
}
// 2. 构建各新节点的 random 指向
cur = head;
while(cur != nullptr) {
if(cur->random != nullptr)
cur->next->random = cur->random->next;
cur = cur->next->next;
}
// 3. 拆分两链表
cur = head->next;
Node* pre = head, *res = head->next;
while(cur->next != nullptr) {
pre->next = pre->next->next;
cur->next = cur->next->next;
pre = pre->next;
cur = cur->next;
}
pre->next = nullptr; // 单独处理原链表尾节点
return res; // 返回新链表头节点
}
};
160. 相交链表
题目理解:
相交指的是指针相同,不是数值相同。如果两个链表相交,那么相交点之后的长度是相同的。两个链表的长度是不同的,所以产生了步频不同步的场景。
思路1:求长度并对齐
求长度--将较长链表指针移至与较短链表头相同位置--开始查找
思路2:循环遍历(尾端对齐)
我们通过循环遍历的方式,使得两个链表从尾端开始向前遍历长度相同。
pA走过的路径为A链+B链
pB走过的路径为B链+A链
pA和pB走过的长度都相同,都是A链和B链的长度之和,相当于将两条链从尾端对齐,如果相交,则会提前在相交点相遇,如果没有相交点,则会在最后相遇。
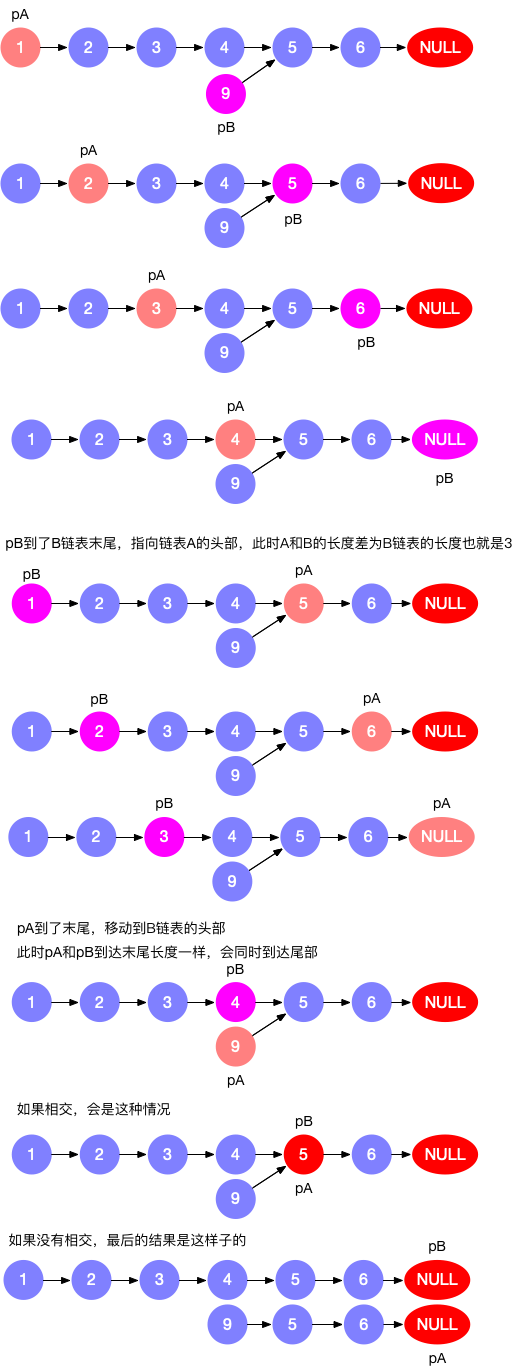
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *A = headA, *B = headB;
while (A != B) {
A = A != nullptr ? A->next : headB;//到当前链表末尾了吗?到了就切换另一条链表,没到就继续递推
B = B != nullptr ? B->next : headA;
}
return A;
}
};
注意声明结点写法
栈和队列
LCR 125. 图书整理 II
题意理解:用两个栈实现一个队列
题目中说:用两个书车来实现借还书的任务,也就是暗示我们借还书分别使用两个书车来完成。题目中还说,为了保持图书的顺序,图书管理员每次取出供读者借阅的书籍是最早归还到图书馆的书籍。你需要返回每次读者借出书的值
所以,基于此需求,我们考虑使用栈来实现。
栈A用于入库图书,栈B用于出库图书,每当有出库需求时,将A中元素依次弹出加入B.若B不为空,则说明B中已存在倒序过的A中元素,继续使用B即可。
155. 最小栈
思路1:辅助栈维护
利用辅助栈维护最小值。
入栈,若当前值小于等于辅助栈顶元素值,则一并加入辅助栈;
出栈,若当前出栈元素等于辅助栈顶元素值,则辅助栈一并弹出栈顶。
思路2:单栈+重复入栈保存状态
当有更小的值来的时候,我们只需要把之前的最小值入栈,当前更小的值再入栈即可。当这个最小值要出栈的时候,下一个值便是之前的最小值了。
那么,如果发生了我们上面说的重复入栈,若出栈的刚好等于min,再次出栈并更新min。这样操作是没有问题的:

思路3**:单栈+int对保存状态
- We push 5,-2,3,-10,20 in the stack.
- If the stack is empty we push {val,val} in the stack
else we push {val,min(s.top().second,val)} which is basically minimum upto that point. - Hence {5,5},{-2,-2},{3,-2},{-10,-10},{20,-10} are pushed in the stack.
946. 验证栈序列
思路:模拟栈
不断向栈中添加元素,直到当前元素与pop数组顶部元素一致,则弹出栈顶元素,pop也弹出栈顶。
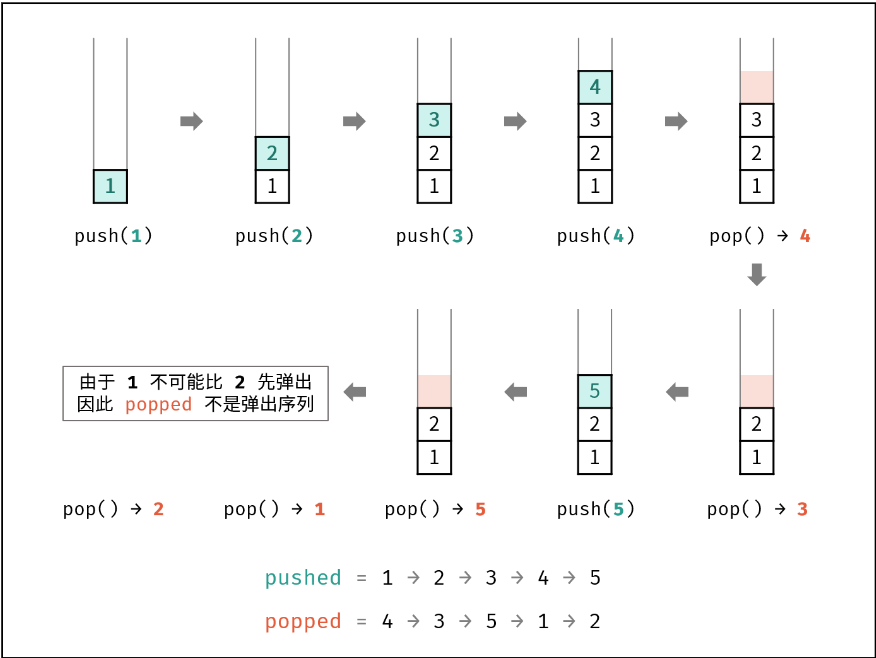
循环判断与出栈:
for (int num : pushed) {
stk.push(num); // num 入栈
while (!stk.empty() && stk.top() == popped[i]) { // 循环判断与出栈
stk.pop();
i++;
}
}
当遇到元素相等时,两者同时“弹出”元素,此时栈内指针由于栈的特性好像在“后移”。
LCR 184. 设计自助结算系统
思路:队列+双端队列维护最值
注意题目要求时间复杂度为O(1)
利用额外变量维护最大值的思路是有缺陷的,因为最大值会因出队而改变。我们无从得知元素出队是否会对最大值产生影响。
所以,我们考虑使用双端队列deque来记录极值,队列首部一定是当前最大值

注意,添加元素操作时,更新最大值的判断操作应该是:
while(!dq.empty() && dq.back()<value){dq.pop_back();}
树
二叉树知识回顾
满二叉树、完全二叉树、二叉搜索树、平衡二叉搜索树(AVL)(它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。)
二叉树定义:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
二叉树遍历方式小结
二叉树遍历主要分为两类:
- 深度优先遍历
- 前序遍历(迭代法、递归法)->DLR
- 中序遍历(迭代法、递归法)->LDR
- 后序遍历(迭代法、递归法)->RLD
- 广度优先遍历
- 层次遍历(迭代法、递归法)
前中后序的递归遍历
按照递归三部曲执行即可:
- 确定函数返回值和传入参数
- 确定终止条件
- 确定单层递归逻辑
//以前序遍历为例
vector.push(noode->val)//处理中间节点逻辑
traversal(node->left)//左
traversal(node->right)//右
前中后序的迭代遍历
迭代法通常需要额外数据结构辅助:栈
这里强调两个概念:访问顺序和操作顺序
前序和后序的访问、处理顺序相同(后序遍历后需对结果数组反序)
//以前序遍历为例
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();// 中
st.pop();
result.push_back(node->val);
if (node->right) st.push(node->right);// 右(空节点不入栈)
if (node->left) st.push(node->left); // 左(空节点不入栈)
}//为什么先入栈右节点?因为栈的数据结构是FILO的,右侧节点先入,后出
而中序遍历这两个顺序不同,对于如下的一颗二叉树:
访问(从根节点开始访问)顺序:5-4-1-2-6
操作(加入结果数组)顺序:1-4-2-5-6
所以我们考虑用栈来记录我们访问过的顺序,一路向左走,直到遇到叶子节点,开始往回走,弹栈,访问栈顶元素的右节点,右节点入栈,重复执行之前的步骤。
如上图所示,沿着5->4->1这条路线一直访问到最左子节点,此时cur->left == null,栈中顺序为541,开始弹栈,弹出1,由于1的右子节点也为空,所以再次弹栈54->4,4的右子节点不为空,2入栈。
while (cur != NULL || !st.empty()) {
if (cur != NULL) {// 指针来访问节点,一路向左访问到最底层
st.push(cur); // 将访问的节点放进栈
cur = cur->left;// 左
} else {
cur = st.top(); // 从栈里弹出的数据,就是要处理的数据
st.pop();
result.push_back(cur->val);// 中
cur = cur->right;// 右
}
}
使用迭代法实现层次遍历
还是上面那颗二叉树,若使用层次遍历,得到的结果集应该是:{[5]、[4、6]、[1、2]}
层次遍历使用的是迭代法,因此也需要额外的数据结构辅助
由于队列符合FIFO的特性,考虑使用队列实现
根5首先加入队列,5弹出队列后,4、6依次加入队列。当前队列大小为2,弹出4,将1、2加入队列。现在队列中元素是612。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};
使用递归法实现层次遍历
class Solution {
public:
void order(TreeNode* cur, vector<vector<int>>& result, int depth)
{
if (cur == nullptr) return;
if (result.size() == depth) result.push_back(vector<int>());
result[depth].push_back(cur->val);
order(cur->left, result, depth + 1);
order(cur->right, result, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
int depth = 0;
order(root, result, depth);
return result;
}
};
105. 从前序与中序遍历序列构造二叉树
思路:递归(分治)
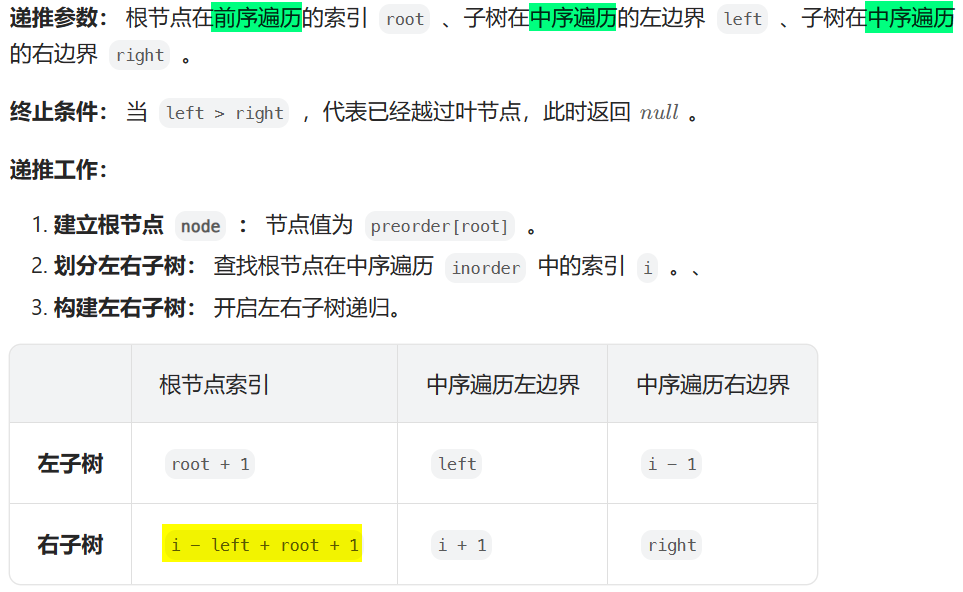
优化:将中序遍历的值和索引保存在哈希表中,把查找的时间复杂度降到O(1)
for(int i = 0; i < inorder.size(); i++)
dic[inorder[i]] = i;
LCR 143. 子结构判断
思路1:回溯
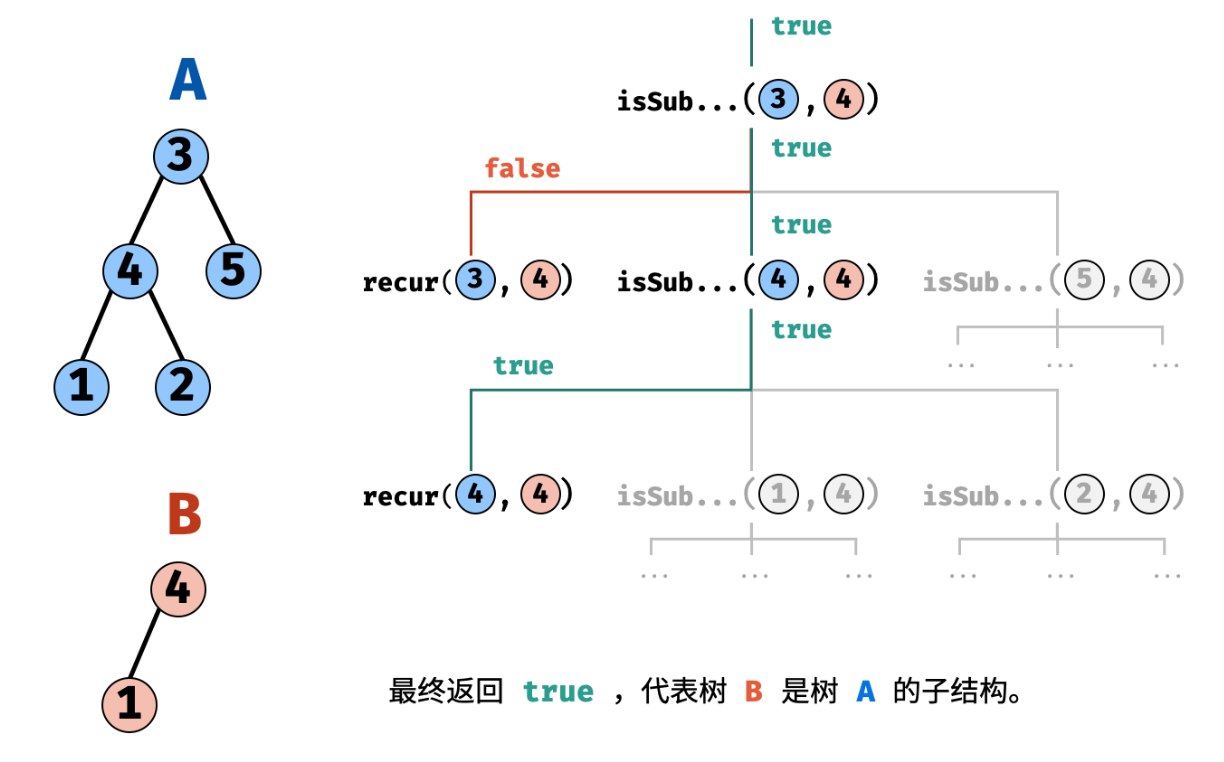
isSubstrcuture():判断B是否为A的子结构,换言之,也就是还没有到逐对比较的地步
recur():开始逐对比较两子树中的元素
由于采用递归,按照递归的步骤分析:
- 递归的终止条件:B结点为空、A结点为空、AB结点值不同
- 返回值:A的左节点和A的右节点分别执行recur函数
bool recur(TreeNode* A, TreeNode* B){
if(B==nullptr) return true;
if(A==nullptr || A->val != B->val) return false;
return recur(A->left,B->left) && recur(A->right,B->right);
}
针对判断函数,B为A的子结构有以下三种可能:
- B的子结构起点为A的根节点,此时结果为recur(A,B)
- B的子结构起点隐藏在A的左子树中,而不是直接为A的根节点,此时结果为isSubStructure(A.left, B)
- B的子结构起点隐藏在A的右子树中,此时结果为isSubStructure(A.right, B)
226. 翻转二叉树
思路1:递归
递归采用的是DFS,不需要额外空间辅助。(一竿子插到底)
借本题回顾递归的三部曲: 1.确定传入参数和返回值
题目已经给出
2.确定终止条件
if(root == nullptr){
return root;
}
3.确定单层递归逻辑
swap(toot->left,root->right);
invertTree(root->left);
invertTree(root->right);
思路2:迭代
迭代采用的是BFS,需要额外的数据结构(队列)来辅助实现。(层层扫荡)
本题考虑使用栈来实现。
LCR 149. 彩灯装饰记录 I
广度优先遍历,通常借助队列实现

102. 二叉树的层序遍历
例题,不多说
LCR 151. 彩灯装饰记录 III
思路1:BFS+双端队列

如何判断奇偶层?
利用res.size()来判别,由于res是二维数组,每次加入结果res.size()就会+1.
如果这个逻辑不好写出,可以考虑将左右情况分开来写:
class Solution {
public:
vector<vector<int>> decorateRecord(TreeNode* root) {
deque<TreeNode*> deque;
vector<vector<int>> res;
if(root != NULL) deque.push_back(root);
while(!deque.empty()) {
// 打印奇数层
vector<int> tmp;
for(int i = deque.size(); i > 0; i--) {
// 从左向右打印
TreeNode* node = deque.front();
deque.pop_front();
tmp.push_back(node->val);
// 先左后右加入下层节点
if(node->left != NULL) deque.push_back(node->left);
if(node->right != NULL) deque.push_back(node->right);
}
res.push_back(tmp);
if(deque.empty()) break; // 若为空则提前跳出
// 打印偶数层
tmp.clear();
for(int i = deque.size(); i > 0; i--) {
// 从右向左打印
TreeNode* node = deque.back();
deque.pop_back();
tmp.push_back(node->val);
// 先右后左加入下层节点
if(node->right != NULL) deque.push_front(node->right);
if(node->left != NULL) deque.push_front(node->left);
}
res.push_back(tmp);
}
return res;
}
};
思路2:双栈法
偶数层的数,让子节点进入奇数层,左边先进,先进先出,弹栈实现从右至左
奇数层的数,让子节点进入偶数层,右边先进,弹栈实现从左至右。
LCR 152. 验证二叉搜索树的后序遍历序列
思路1:递归分治
若子树都满足后序遍历特点,那么整棵树也一定满足。
如何拆分数组?
根据后序遍历的特点,末尾的元素一定是根节点,我们只需要从右至左寻找第一个大于此节点的节点,即可划分左右子树。
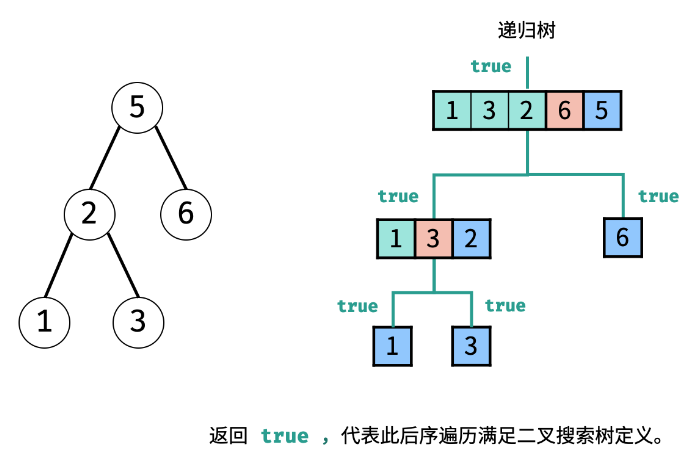
寻找左右子树和决断条件:
if(i >= j) return true;
int p = i;
while(postorder[p] < postorder[j]) p++;
int m = p;
while(postorder[p] > postorder[j]) p++;
思路2:辅助栈(比较难理解,还是用递归吧~)
观察倒序的后序遍历数组,我们不难发现,挨着的两个数如果arr[i]<arr[i+1],那么arr[i+1]一定是arr[i]的右子节点。同样是基于这个倒序的数组,如果arr[i]>arr[i+1],那么arr[i+1]一定是arr[0]……arr[i]中某个节点的左子节点,并且这个值是大于arr[i+1]中最小的。
LCR 155. 将二叉搜索树转化为排序的双向链表
思路:中序遍历
首先需要明确题目对我们的要求:排序+双向+循环链表
根据题目的排序要求,本题提供的树型结构又是搜索二叉树,所以我们不难想到使用中序遍历的遍历次序,这样得到的序列自然具备升序。

if(pre!=nullptr) pre->right=cur;//pre用于记录pre左侧的节点,若pre为空,则说明pre应该在整棵树的左下侧,即为双向链表的头结点
else head=cur;
cur->left=pre;
pre=cur;//为遍历右侧子树做准备,pre应当指向当前节点
297. 二叉树的序列化与反序列化
思路:层序遍历
只有层序遍历才能完整携带二叉树信息。
针对序列化后的表达式,我们不难发现如下规律:
序列化:
string serialize(TreeNode* root) {
string res;
if (!root) return res;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* front = q.front();
q.pop();
if (front) {
res += to_string(front->val) + ",";
q.push(front->left);
q.push(front->right);
}
else res += "null,";
}
return res.substr(0, res.size() - 1);
}
反序列化:
反序列化的操作略有不同:
- 首先要去掉首尾的[]并去掉间隔的,
- node入队
- 构建node的左子结点,i++
- 构建node的右子结点,i++
TreeNode* deserialize(string data) {
if (data.empty()) return nullptr;
vector<string> s = split(data);//去掉首尾[]并去掉间隔的,
queue<TreeNode*> q;
TreeNode* root = new TreeNode(stoi(s[0]));
q.push(root);
int i = 1;
while (!q.empty()) {
TreeNode* front = q.front();
q.pop();
if (s[i] != "null") {
front->left = new TreeNode(stoi(s[i]));
q.push(front->left);
}
++i;
if (s[i] != "null") {
front->right = new TreeNode(stoi(s[i]));
q.push(front->right);
}
++i;
}
return root;
}
LCR 174. 寻找二叉搜索树中的目标节点
思路1:二叉搜索树+第N大->栈,中序遍历
思路2:维护cnt变量+逆序中序遍历
if(root == nullptr) return;
dfs(root->right);
if(cnt == 0) return;//越界
if(--cnt == 0) res = root->val;//找到结果
dfs(root->left);
104. 二叉树的最大深度
层序遍历,略。
110. 平衡二叉树
平衡二叉树是指该树所有结点的左右子树深度差不超过1
二叉树的深度为:当前树的深度=max(左子树深度,右子树深度)+1
思路1:后序遍历+剪枝

return abs(left - right) < 2 ? max(left, right) + 1 : -1;
剪枝操作:
int left = recur(root->left);
if (left == -1) return -1;
int right = recur(root->right);
if (right == -1) return -1;
思路2:先序遍历+多重判断
判断:当前子树是否是平衡+当前子树左子树是否平衡+当前子树右子树是否平衡
abs(depth(root->left)-depth(root->right)) <= 1 && isBalanced(root.left) && isBalanced(root->right);
235. 二叉搜索树的最近公共祖先
思路1:非递归解决
对于二叉搜索树,我们应该认识到:
- 如果两个节点值都小于根节点,说明他们都在根节点的左子树上,我们往左子树上找
- 如果两个节点值都大于根节点,说明他们都在根节点的右子树上,我们往右子树上找
- 如果一个节点值大于根节点,一个节点值小于根节点,说明他们他们一个在根节点的左子树上一个在根节点的右子树上,那么根节点就是他们的最近公共祖先节点。
然后逐渐改变root的值.
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while (root != nullptr) {
if (root->val < p->val && root->val < q->val) // p,q 都在 root 的右子树中
root = root->right; // 遍历至右子节点
else if (root->val > p->val && root->val > q->val) // p,q 都在 root 的左子树中
root = root->left; // 遍历至左子节点
else break;
}
return root;
}
思路2:递归解决
将上述思路改为递归即可
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root->val < p->val && root->val < q->val)
return lowestCommonAncestor(root->right, p, q);
if (root->val > p->val && root->val > q->val)
return lowestCommonAncestor(root->left, p, q);
return root;
}
};
思路3:通用递归解法(不利用二叉搜索树性质)
if(root == nullptr || root == p || root == q) return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if(left == nullptr) return right;
if(right == nullptr) return left;
return root;
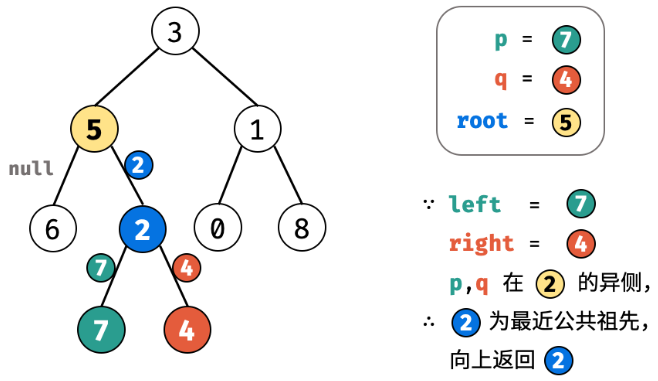
236. 二叉树的最近公共祖先
参考上题思路3.
小结:利用对称性递归解决二叉树判断问题
问题分类
不需要构造函数:
- 单树问题,不需要用到子树的某一部分,只需要利用根节点的左右子树的对称性
- 双树问题,题目要求比较两棵树
参考:
- 相同的树
- 翻转二叉树
- 二叉树的最大深度
- 平衡二叉树
- 二叉树的直径
- 合并二叉树
- 另一个树的子树
- 单值二叉树
需要构造辅助函数:
- 必须要用到子树的某一部分进行递归,形式上主函数单参,辅助函数双参
- 参考:
- 对称二叉树
- 剑指 Offer 26. 树的子结构
解题模板
递归结束条件:特殊情况判断
如果是单树问题:
if(!root) return true/false;
if(!root->left) return true/false/递归函数;
if(!root->right) return true/false/递归函数;
如果是双树问题:
if(!p && !q)return true/false;
if(!p || !q)return true/false;
具体问题需要具体分析
返回值:通常是多个条件的复合判断语句
非空判断、结点值比较、(单树)调用根节点左右子树的递归函数进行递归判断、(双树)调用两棵树的左右子树的递归函数进行判断
排序算法
| 冒泡排序 | 插入排序 | 选择排序 | 快速排序 | 归并排序 |
|---|---|---|---|---|
| 稳定 | 稳定 | 不稳定 | 不稳定 | 稳定 |
冒泡排序
冒泡排序每次只对相邻两个元素进行操作。每次冒泡操作,都会比较相邻两个元素的大小,若不满足排序要求,就将它俩交换。每一次冒泡,会将一个元素移动到它相应的位置,该元素就是未排序元素中最大的元素。

void BubbleSort(vector<int>& arr) {
for (int i = 0; i < arr.size() - 1; i++)
for (int j = 0; j < arr.size() - i - 1; j++)
if (arr[j] > arr[j+1])
swap(arr[j], arr[j+1]);
}
效率优化:
若某一轮中没有进行任何交换操作,则说明后续轮数中也不会进行加交换,故可设置标志位。
稳定性:
稳定的,遇到相等元素不交换
时间复杂度: O(n^2)
插入排序
与向有序数组中加入元素类似,每次加入时都需要先于原数组中的元素比较,找到应该插入的位置,将后续元素移动后,插入元素。
插入排序维护了两个区间,一个是有序区间,最开始只有最左侧的元素;一个是无序区间,最开始维护的是除首元素之外的元素。

稳定性:
稳定的,遇到相等元素不交换
时间复杂度: O(n^2)
许多编程语言(例如 Java)的内置排序函数采用了插入排序,大致思路为:对于长数组,采用基于分治策略的排序算法,例如快速排序;对于短数组,直接使用插入排序。
void InsertionSort(vector<int>& arr, int len) {
for (int i = 1; i < len; ++i) { //注意i从1开始
int key = arr[i]; //需要插入的元素
int j = i - 1; //已排序区间
while ((j >= 0) && (arr[j] > key)) {
arr[j + 1] = arr[j]; //元素向后移动
j--;
}
arr[j + 1] = key;
}
}
选择排序
与插入排序类似,都维护了两个区间,但是选择排序不涉及元素移动,而是以交换元素来使元素有序。注意:遍历未排序区间需要找到小于当前比较元素的最小元素。

void SelectionSort(vector<int>& arr) {
for (int i = 0; i < arr.size()-1; i++) {
int min = i;
for (int j = i + 1; j < arr.size(); j++)
if (arr[j] < arr[min]) min = j;
swap(arr[i], arr[min]);
}
}
稳定性:
不稳定,跨大量元素交换
时间复杂度: O(n^2)
快速排序
分治
每一层优先选出pivot(枢纽),将小于pivot的元素放在左侧,大于其的元素放在右侧,递归划分左右数组。
我们每次指定pivot指向最后一个元素(最左也可以),同时定义一个变量location,用来标记pivot最后应该置于的位置。在location左侧的所有元素都是比pivot值小的,从location开始,右侧所有元素都比pivot大。
只要遍历到的元素比pivot的值小,就与location所指的元素进行交换,同时location++,更新pivot应该在的位置。
数组遍历结束,最后将元素pivot与location所指元素进行交换,这样,pivot左侧的元素就全部比pivot小,右侧元素全部比pivot大了。
int partition(vector<int>& arr, int left, int right) {
int pivot = right;
int location = left;
for (int i = left; i < right; i++) {
if (arr[i] < arr[pivot]) {
int temp = arr[i]; arr[i] = arr[location]; arr[location] = temp;
location++;
}
}
int temp = arr[pivot]; arr[pivot] = arr[location]; arr[location] = temp;
return location;
}
void QuickSort(vector<int>& arr,int left, int right) {
if (left >= right) return;
int pivot = partition(arr, left, right);
QuickSort(arr, left, pivot-1);//划分
QuickSort(arr, pivot + 1, right);
}
时间复杂度: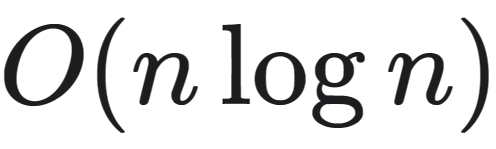
稳定性:不稳定
图解:
归并排序
分治的典型应用
将数组不断从中点处拆分,当子数组长度为一时停止拆分,开始向上合并。
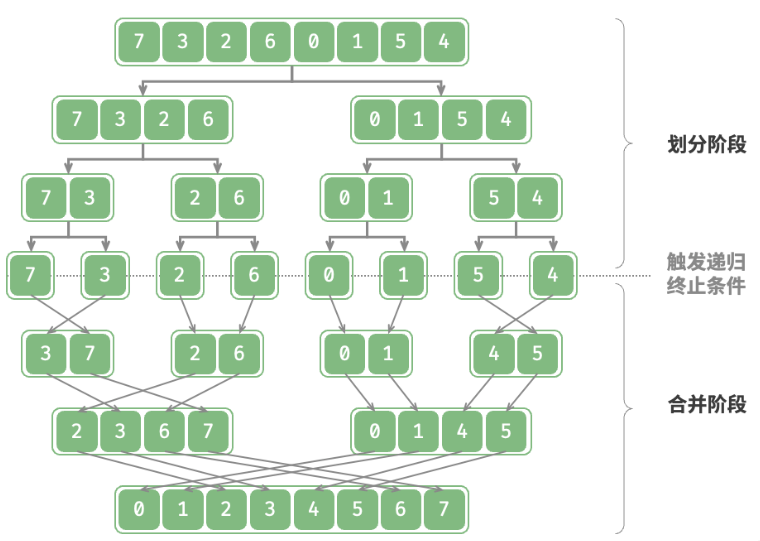
合并结果与二叉树后序遍历一致。
void merge(vector<int> &nums, int left, int mid, int right) {
// 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]
// 创建一个临时数组 tmp ,用于存放合并后的结果
vector<int> tmp(right - left + 1);
// 初始化左子数组和右子数组的起始索引
int i = left, j = mid + 1, k = 0;
// 当左右子数组都还有元素时,进行比较并将较小的元素复制到临时数组中
while (i <= mid && j <= right) {
if (nums[i] <= nums[j])
tmp[k++] = nums[i++];
else
tmp[k++] = nums[j++];
}
// 将左子数组和右子数组的剩余元素复制到临时数组中
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
for (k = 0; k < tmp.size(); k++) {
nums[left + k] = tmp[k];
}
}
void mergeSort(vector<int> &nums, int left, int right) {
if (left >= right)
return;
int mid = left + (right-left)/2;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
时间复杂度: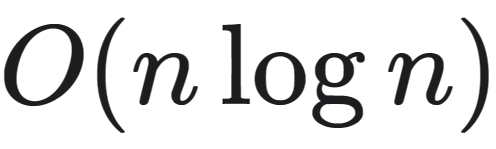
稳定性:稳定
位运算
191. 位1的个数
思路1:库函数(不推荐)
class Solution {
public:
int hammingWeight(uint32_t n) {
bitset<32> bset(n);
return bset.count();
}
};
思路2:无脑做法
但,注意vector数组在没有分配空间时,不能通过下标访问。
//错误写法
res[n]=n%2;
//正确写法
res.push(n%2);
思路3:利用右移运算符
逻辑右移:>>舍弃最低位,高位用符号位填补
算术右移:>>>舍弃最低位,高位补0
以上是针对Java语言的实现,C++语言中逻辑右移和算数右移共享同一个运算符
>>。编译器决定使用逻辑右移还是算数右移,根据的是运算数的类型。如果运算数类型是unsigned则采用逻辑右移,而signed则采用算数右移。
这道题我们应该考虑采用逻辑右移,否则对于负数而言,二进制高位永远是1,n永远不可能为0,造成死循环。
while (n != 0) {
res += n & 1;
n >>= 1;
}
思路4:技巧-消除二进制末尾的1
利用&运算符,使得n和n-1执行位与运算,这个操作可以使n的最后一个1位置上的1变为0.
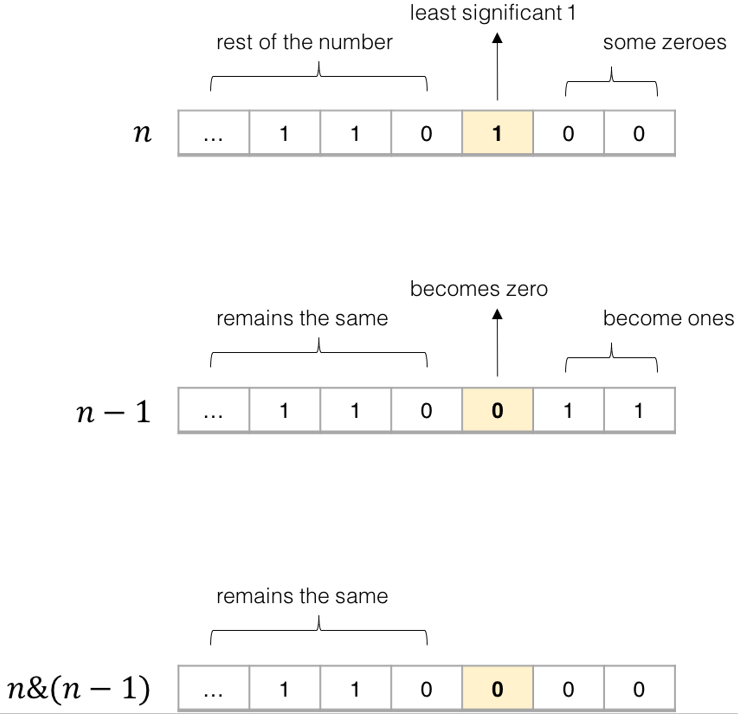
while(n! =0){//n!=00000000
res+ +;
n&=n-1;
}
为什么此处的n!=0能理解成n!=00000000? 因为若运算符一侧为有符号数,另一侧为无符号数,C语言将发生隐式类型转换。(有符号->无符号)
# bit操作
& 符号,x & y ,会将两个十进制数在二进制下进行与运算
| 符号,x | y ,会将两个十进制数在二进制下进行或运算
^ 符号,x ^ y ,会将两个十进制数在二进制下进行异或运算
<< 符号,x << y 左移操作,最右边用 0 填充
>> 符号,x >> y 右移操作,最左边用 0 填充
~ 符号,~x ,按位取反操作,将 x 在二进制下的每一位取反
# 整数集合set位运算
# 整数集合做标志时,比如回溯时的visited标志数组
vstd 访问 i :vstd | (1 << i)
vstd 离开 i :vstd & ~(1 << i)
vstd 不包含 i : not vstd & (1 << i)
并集 :A | B
交集 :A & B
全集 :(1 << n) - 1
补集 :((1 << n) - 1) ^ A
子集 :(A & B) == B
判断是否是 2 的幂 :A & (A - 1) == 0
最低位的 1 变为 0 :n &= (n - 1)
最低位的 1:A & (-A),最低位的 1 一般记为 lowbit(A)
50. Pow(x, n)
思路1:快速幂
使用快速幂法可将时间复杂度由n->logn

我们如何得到到底是哪几个幂次相乘呢?
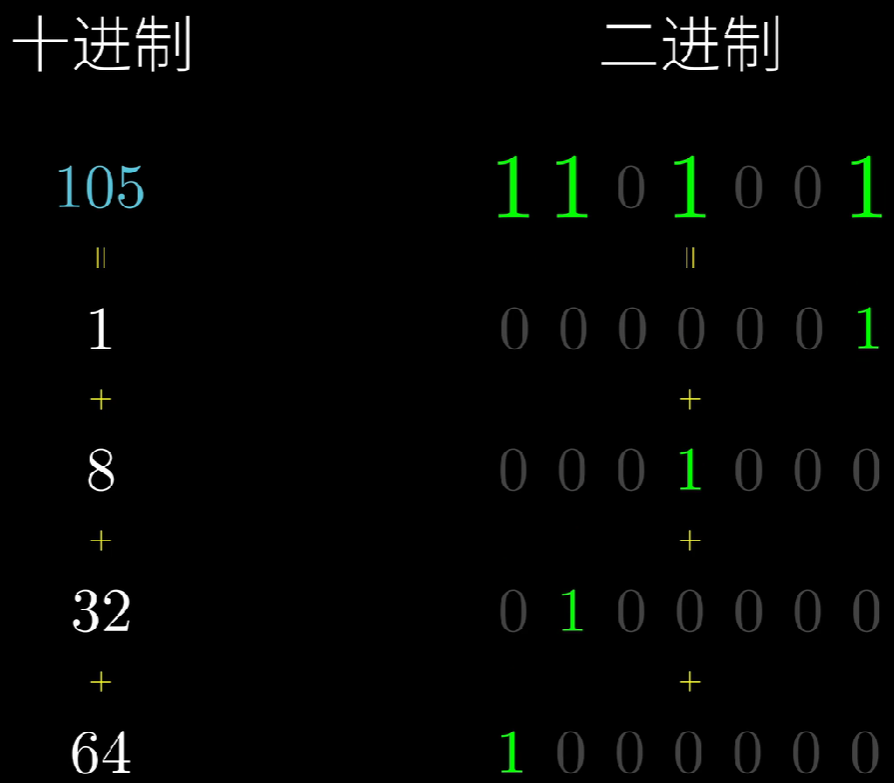
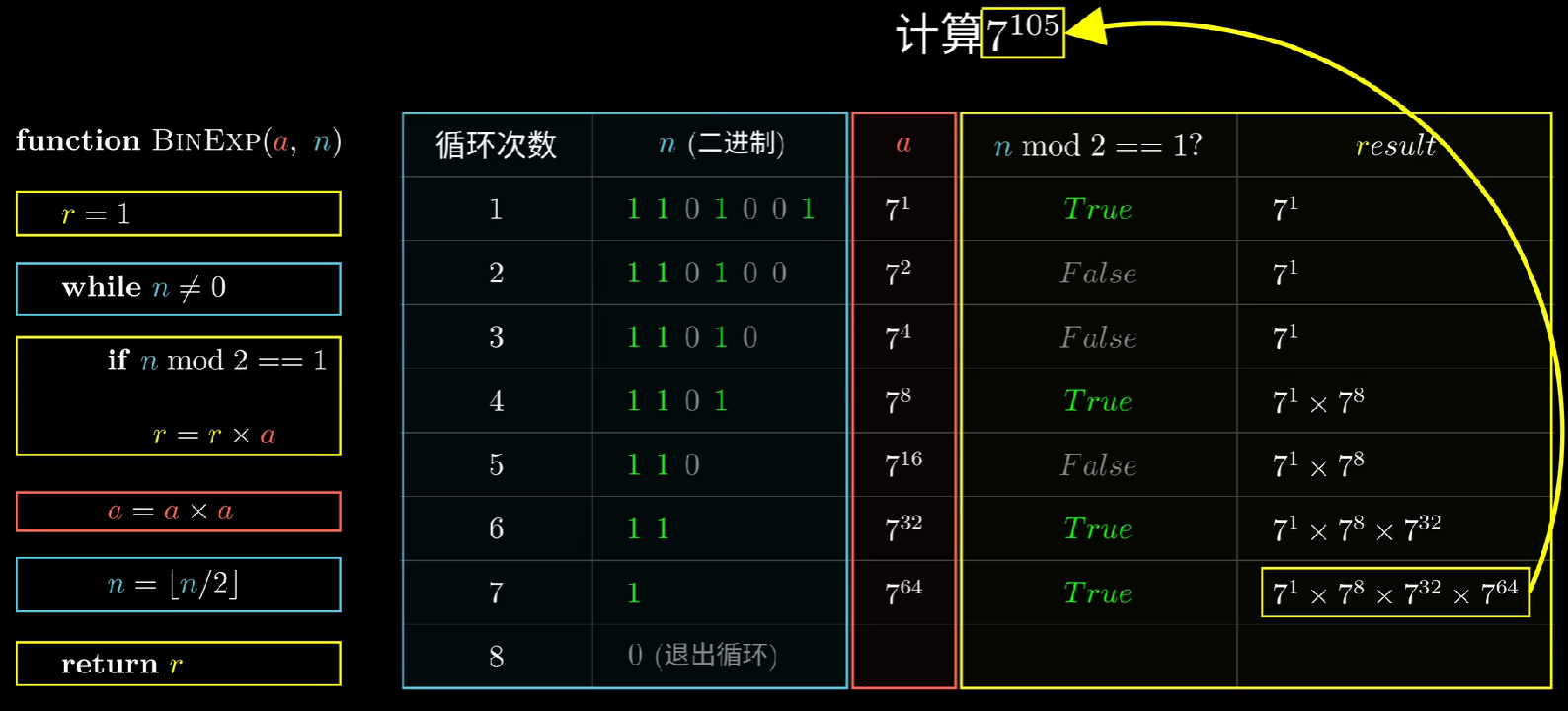
将105的二进制表达逐渐去掉最后一位(n=n/2),若本次去掉的位为1(n mod 2 == 1?),则执行累乘操作(r=r X a),否则略过。
数学解释:

思路2:二分递归
我们可以将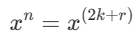 执行以下的分解操作:
执行以下的分解操作:
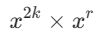
这里的2k可以通过n/2得到k,再将这个结果累乘即可。而r可以通过n mod 2实现。
LCR 177. 撞色搭配
思路1:双指针
需要额外注意的是,若遇到相同数字,两个指针需要同时向后移动两位。
思路2:异或运算
异或运算的性质是:两个相同的数字,异或运算为0.若将数组内所有元素执行异或运算,得到的将是出现一次的数字。
但这只适用于一个独特数字的情况,所以我们考虑将原数组拆分为两个新数组。
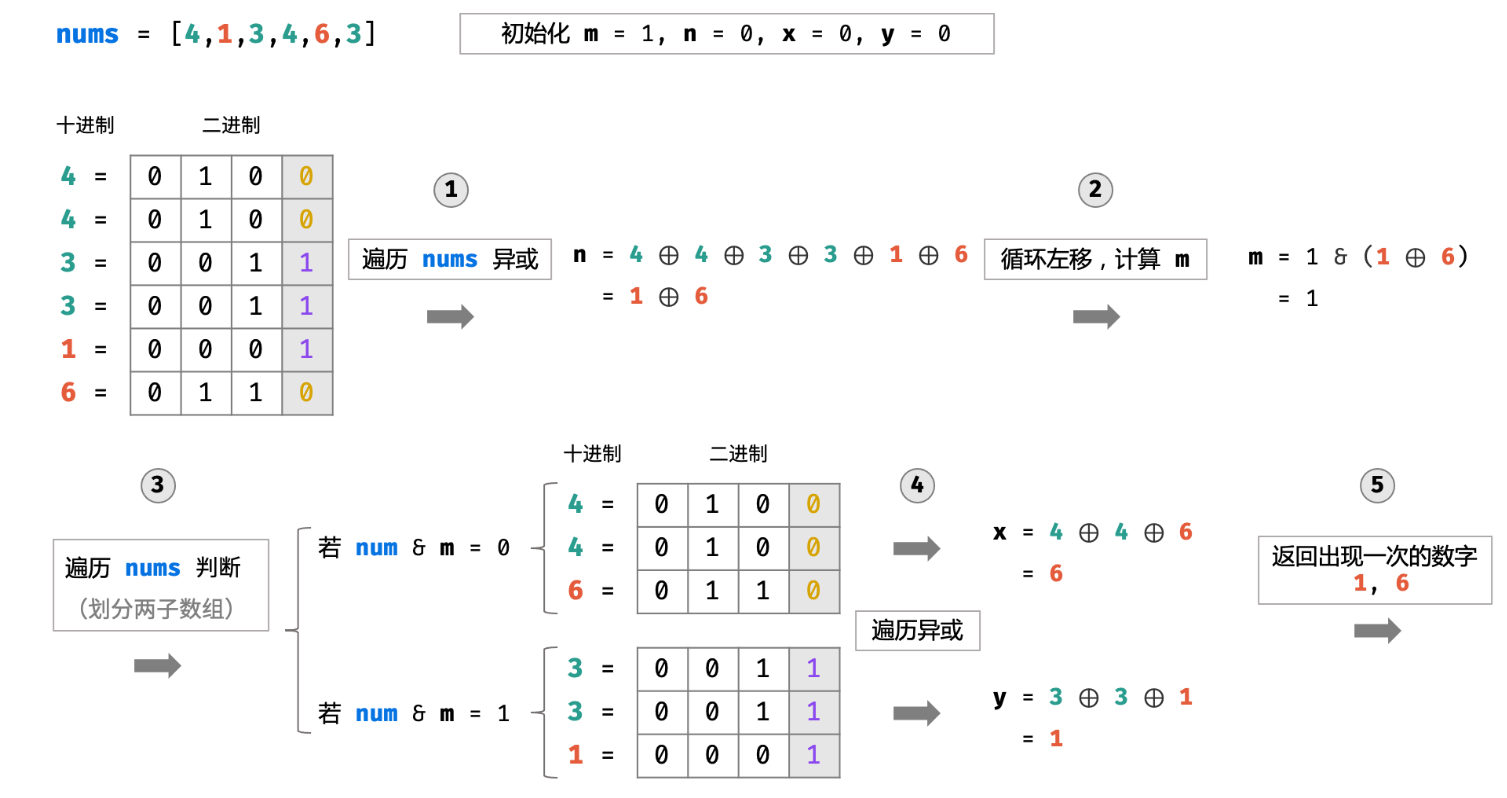
我们获得X异或Y的结果后,要思考的是如何将这两数分开? 当我们把数组分为两组进行异或时,就能知道到底是哪两个不同的数了
那么如何进行分组呢?我们知道:X和Y必然有一位不同,我们可以利用此来分数组,那么,数组中元素分别与此位进行与操作,即:
if(num & m) x ^= num; else y ^= num;
LCR 178. 训练计划 VI
思路1:移位法
三位为一次跳跃
for (int i = 0; i < (int)nums.size() - 2; i += 3)
if (nums[i] != nums[i + 2]) return nums[i];
思路2:位运算
我们把每位上的0/1加起来模3,若不为0,则说明我们要找的数在本位也不为0.
for(int i = 0; i < 32; ++i){
int cnt = 0;
for(int n : nums){
// n & 1 << i 的值大于0即为真,判断本位是否为1
if(n & (1 << i)) cnt++;
}
// 构造只出现一次的那个数字,采用异或的方法生成二进制中的每一位
if(cnt % 3 == 1) ans ^= (1 << i);
}
n & (1 << i): 1<<i,将1向左移动i位,等效于在i+1位放一个1.将n与此进行与运算,若原数位上为1,结果才会**大于1.**实现了判断对应二进制位是否为1的功能。下部分为结果对应二进制位赋值同理。
LCR 190. 加密运算
思路1:位运算实现全加器 简单的进行异或运算并未考虑到进位的情况。
稍作观察不难发现,当不存在进位时,我们的猜想是正确的.当发生进位时,我们应当采用与运算来计算,并左移一位。
所以我们只要循环求本位和与进位即可,直到进位为0.
若是负数的情况,本方法同样适用,因为无论是正数还是负数,在计算机内的存储形式都是补码。
while (b) {
int carry = a & b; // 计算 进位
a = a ^ b; // 计算 本位
b = (unsigned)carry << 1;//进位数要乘以权值,也就是2。并在下一次相加
}
整体左移,交错相加
动态规划
DP的主要内容还是参看《代码随想录》实体书
LCR 126. 斐波那契数
复习一下动态规划五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
for(int i=2;i<=n;i++)
注意题目要求:sum = (a+b)% 1000000007;
思路1:常规DP
思路2:递归
343. 整数拆分
思路1:数学推导
思路2:动态规划
本题的难点在于,如何推导dp递推公式。题干中提示到:给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),不一定只能拆分为两个数,可以拆分为两个以上的数。
于是我们不难得出:
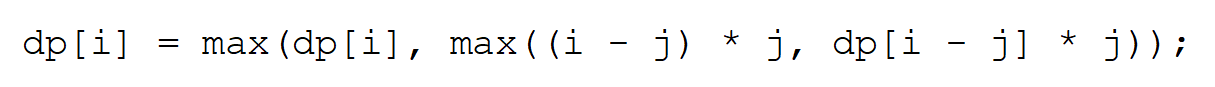
后面两项的含义是要么拆成两个数(j*(i-j)),要么拆成多个数相乘(dp[i-j]*j)。
发现这个规律后,想必dp的初始化,dp的递推方向也不难得出。
为什么dp[i]也要加入最大值的比较中?
因为内层循环时,dp[i]也在不断更新。
图
79. 单词搜索
思路:DFS+剪枝
针对于此题,DFS的顺序应该是:上->下->左->右(图中第一行元素因为没有上方元素直接略过向上访问步骤)

整个递推过程的终止条件为:
- 行或列索引越界
- 当前元素已经访问过
- 当前矩阵元素与目标字符不同
注意,讲匹配过的字符置空应该采用'\0'字符。

3:标记过的点恢复原状,以便进行下一次搜索
LCR 130. 衣橱整理
思路:DFS+剪枝
注意,回溯返回时,需要将本轮结果计入,即:
1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj, visited, m, n, cnt) +dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8, visited, m, n, cnt);
另外,为了使用m和n变量,需要每次都重新传入。
54. 螺旋矩阵
思路:简单模拟
左-右-下-上的顺序进行模拟
注意在执行完每个方向的遍历后,应该进行剪枝操作。
//left->right...
if (++t > b) break;


Comments NOTHING