数组中前缀范围与完全二叉树的对应
数组的前缀范围可以与完全二叉树基本对应,以额外变量size来控制范围: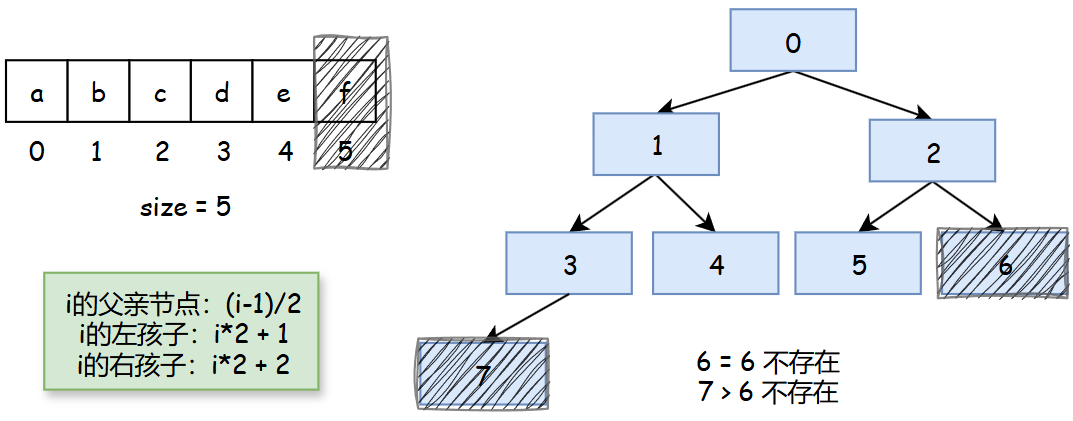
堆结构
堆可以认为是在数组上的,规定好组织方式的完全二叉树。
- 大根堆:任何一个子结构都应满足最大值在顶部
- 小根堆:任何一个子结构都应满足最小值在顶部
heapInsert(向上调整)
heapInsert是将新插入元素做调整以保证大根堆特性的过程。
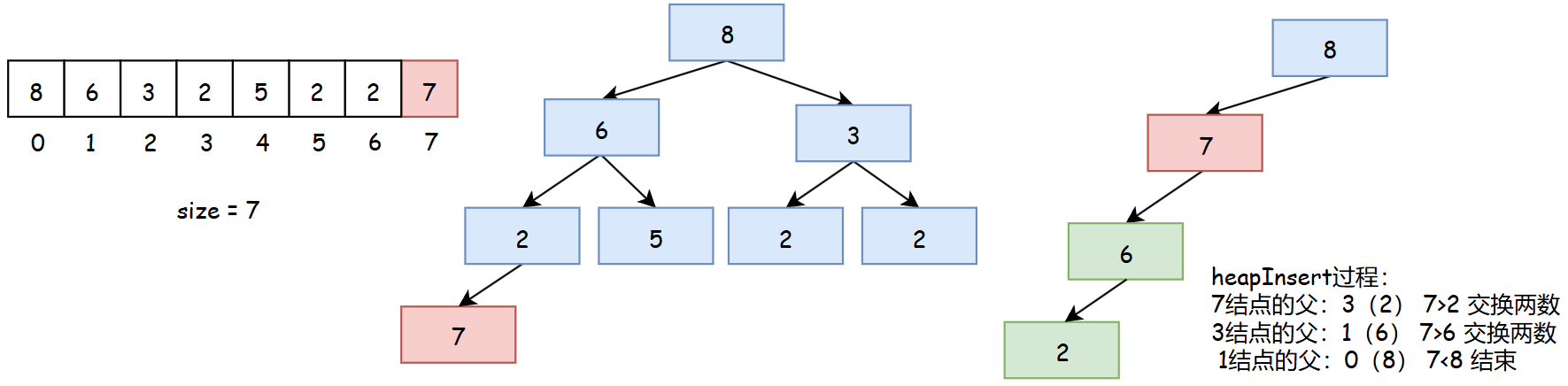
public static void heapInsert(int i) {
while (arr[i] > arr[(i - 1) / 2]) {
swap(i, (i - 1) / 2);
i = (i - 1) / 2;
}
}heapify(向下调整)
heapify是将新变动元素做调整以保证大根堆特性的过程。
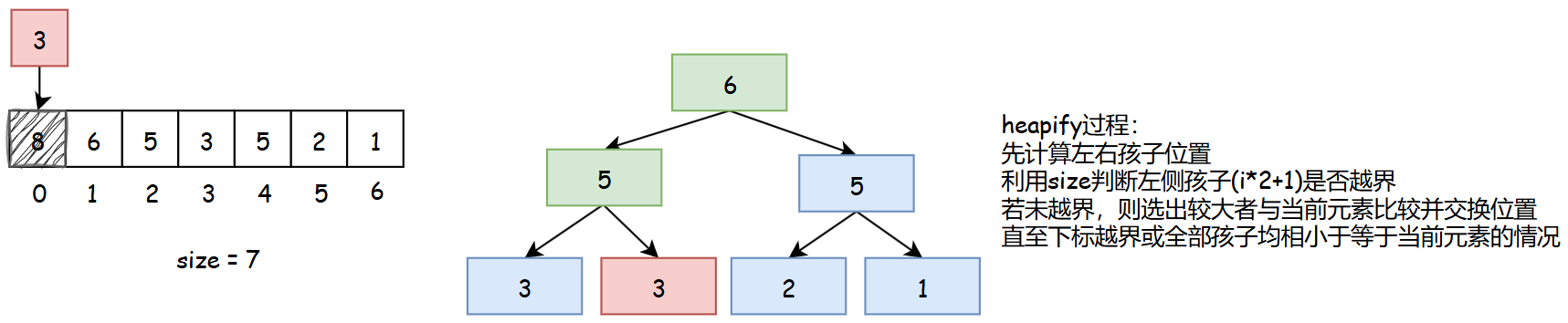
public static void heapify(int i, int size) {
int l = i * 2 + 1;
while (l < size) {
int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
best = arr[best] > arr[i] ? best : i;
if (best == i) {
break;
}
swap(best, i);
i = best;
l = i * 2 + 1;
}
}若只有单侧孩子且值大于当前值,则直接认为单侧孩子是最大的,与当前元素做交换。
时间复杂度分析
不管一个结点怎么调整,都只与自己所在的那一条树枝有关,节点数为N的完全二叉树高度为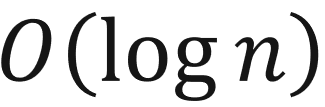 向上取整,所以以上两个过程的时间复杂度均为
向上取整,所以以上两个过程的时间复杂度均为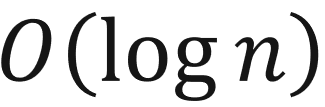 这与完全二叉树本身结构也有关。
这与完全二叉树本身结构也有关。
堆排序
堆排序的过程如下:
- 按照构建大根堆的方式,将待排序数组中的每个元素加入大根堆,每次size++
- 大数归位阶段:将上面步骤中的根节点(最大元素)与最后一个(数组)下标的元素交换,size--,即之后这个最大元素被排除出堆的范围,不参与堆调整
- 由于最小元素被移至堆顶,需要执行heapify过程将其向下移动,保证大根堆特征
- 循环执行上述过程,直至size==0
public static void heapSort1() {
for (int i = 0; i < n; i++) {
heapInsert(i);
}
int size = n;
while (size > 1) {
swap(0, --size);
heapify(0, size);
}
}时间复杂度分析
从顶到底建堆,时间复杂度: (分析:倍增分析法)
(分析:倍增分析法)
时间复杂度O(n * log n),不管以什么方式建堆,调整阶段的时间复杂度都是这个,所以整体复杂度也是这个。
额外空间复杂度是O(1),因为堆直接建立在了要排序的数组上,所以没有什么额外空间。
倍增分析法
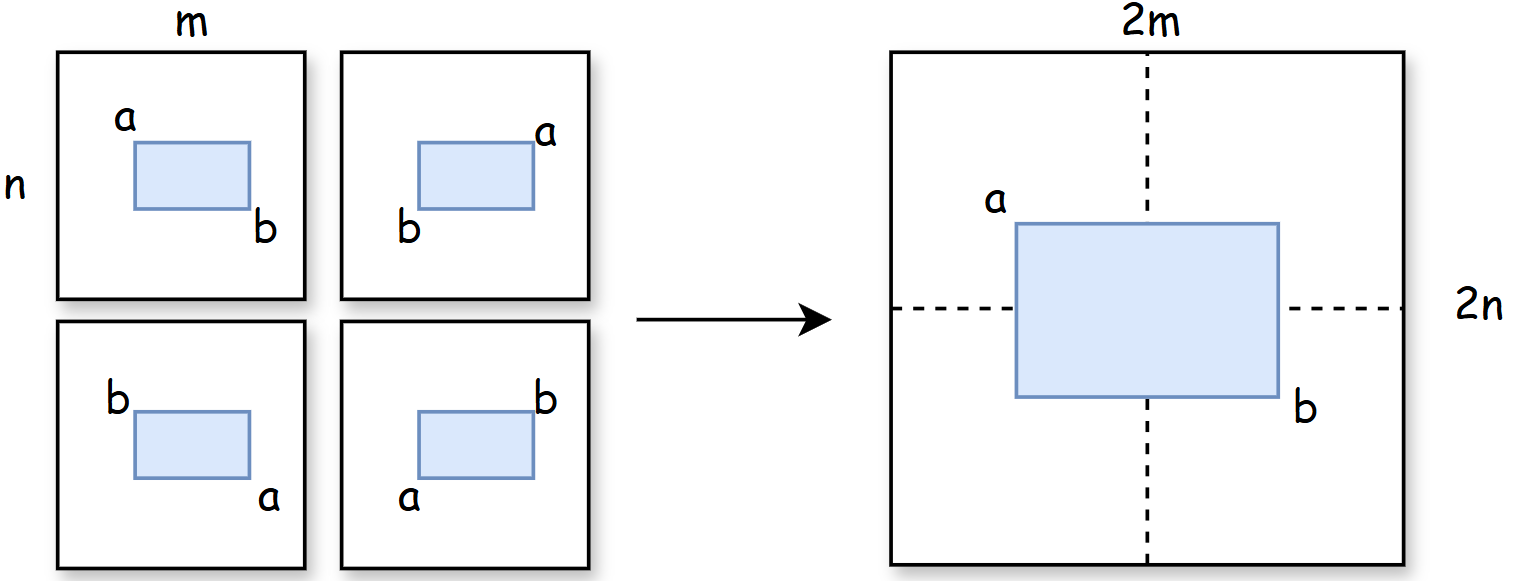
设想有一 n *m大小的矩阵,请求出内部不同则矩阵(矩形)的个数。
两点就可以确定一个矩形,但对于同一个矩形,不同的点选法一共有四种。所以求个数的算法的时间复杂度是O(n^2^ * m^2^),对应能找到的不同矩形的个数是(n^2^ * m^2^)/4,这是普通分析的思路。
现在,我们将原n*m矩阵扩张成2n、2m的规模,原矩阵是以O(n^2^ * m^2^)作为其时间复杂度上限,扩张之后,则是以O(n^2^ * m^2^)作为其下限,因为同一个矩形这时就有四种不同构造方法了,即(4n^2^ * m^2^)/4=O(n^2^ * m^2^)。
我们知道,常数项在时间复杂度计算中是可以忽略不记的,那么在一倍面积下以O(n^2^ * m^2^)做上限,在四倍面积下以O(n^2^ * m^2^)做下限,说明该算法的时间复杂度就是O(n^2^ * m^2^)。

Comments NOTHING