（一二元）子串子序列操作问题

本文针对动态规划部分的子序列、子数组的有关问题做分析。

连续序列（子串）问题

序列问题通常指的是操作对象是原对象的完整、连续的一部分的问题，常见的题目名称：最长连续递增序列、最长重复子数组（数组本身不可拆分，所以子数组一定是原数组的连续的一部分）等。

以674. 最长连续递增序列 - 力扣（LeetCode）为例，题目要求在原数组中找出最长的连续且递增的子序列，根据动态规划的核心思想，我们在访问原数组的第i位元素时，只需要考虑与其前一位数的大小关系，即if (nums[i] > nums[i - 1])，因为dp[i]的含义就是以 i-1 位置元素结尾的最长连续递增子序列长度，而不用像在300. 最长递增子序列 - 力扣（LeetCode）中还需考虑该元素位置之前的所有元素，这就是序列（连续）问题的关键。

本题可以解答如下：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        int result = 1;
        vector<int> dp(nums.size() ,1);
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) { // 连续记录
                dp[i] = dp[i - 1] + 1;
            }
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

再来看一道以数组为背景的题目718. 最长重复子数组 - 力扣（LeetCode），该题目要求找出两个数组中的最长重复子数组，与上面题目的差异是，本题原数组有两个，也就是一个二元问题。

与上面问题相似的是，我们都以邻近元素作为比较条件，不需要再遍历之前的元素来决定当前位置的值，即nums1[i - 1] == nums2[j - 1]，我们将dp[i][j]定义为以 i-1 结尾和以 j-1 结尾的子数组的最长重复长度，解答如下：

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

:::info
至于为什么要将dp[i][j]定义为以 i-1 结尾和以 j-1 结尾的子数组的最长重复长度，这只是一个习惯问题，因为我们遍历元素时，也是从 1 号位置开始的，具体可以看下面的示意图：

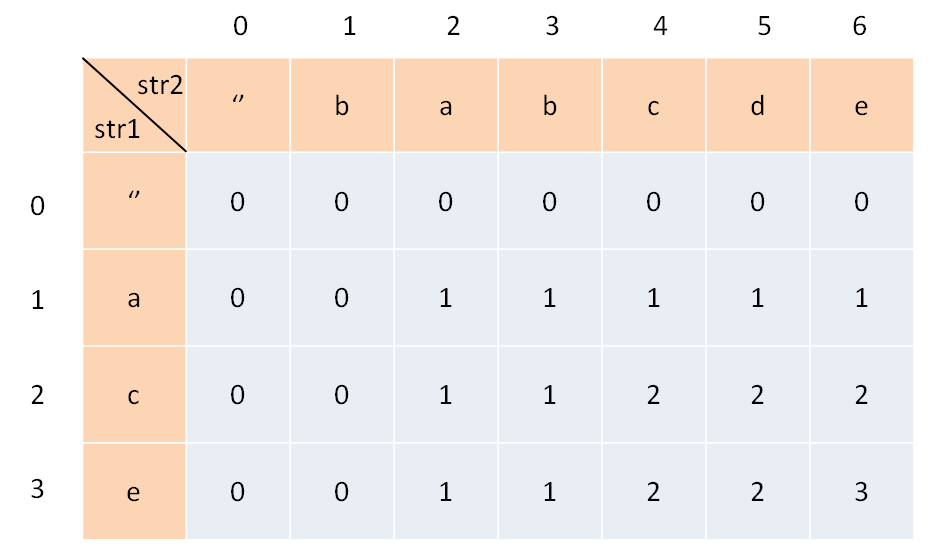
非连续序列（子序列）问题

所谓非连续，也就是说选取的子序列中的元素不一定在原序列中是紧挨着地，比如下面这段题目描述：

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

我们先从前面拿来对比的300. 最长递增子序列 - 力扣（LeetCode）说起，题干给出的示例原数组为： <font style="color:#000000;">[0,3,1,6,2,2,7]</font>，当我们遍历到元素 6 时，由于子序列中元素可以不连续，所以当前位置的 dp 值应该考虑该位置之前的所有元素的 dp 值，即<font style="color:#000000;">dp[i] = max(dp[i], dp[j] + 1)</font>，解答如下：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if (dp[i] > result) result = dp[i]; // 取长的子序列
        }
        return result;
    }
};

再来看一个问题：1143. 最长公共子序列 - 力扣（LeetCode），选择这个问题是为了与上面的最长公共子数组问题作比较。题目要求与上题类似，涉及到二元问题，dp 规模往往都是二维的，此处我们选择将 dp 数组定义为：dp[i][j]:序列 1 的 i-1 位置和序列 2 的 j-1 位置能产生的最长公共子序列长度。那么本题的状态方程该怎么写呢？参考上面的思路，要是i-1和j-1位置字符相同，那还比较简单：

if (text1[i - 1] == text2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + 1;
}

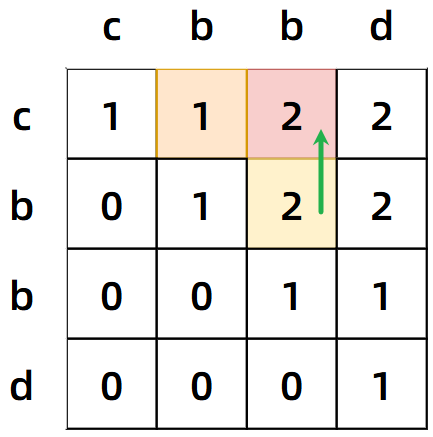
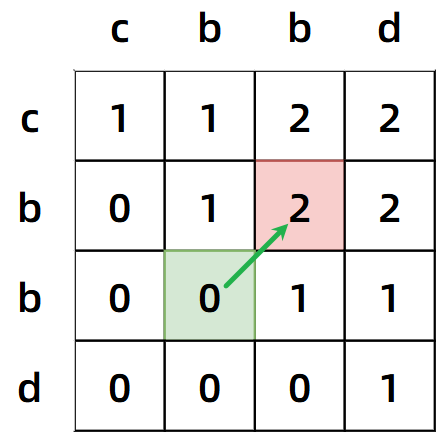
关键就在于若前一个字符不匹配的情况，难道我们也要遍历之前的所有元素吗？考虑以下两个位置（dp 二维矩阵中）dp[i-1][j]和dp[i][j-1]，在下图中也就是橙色和粉色区域，由于 dp 数组的状态传递性，我们没有必要回去查找比较每一个元素，只用看其中一个序列缺省当前元素的最大值即可，放在下图中，橙色区域表示ac和b的最长公共子串长度，粉色区域表示a和ba的最长公共子串长度。

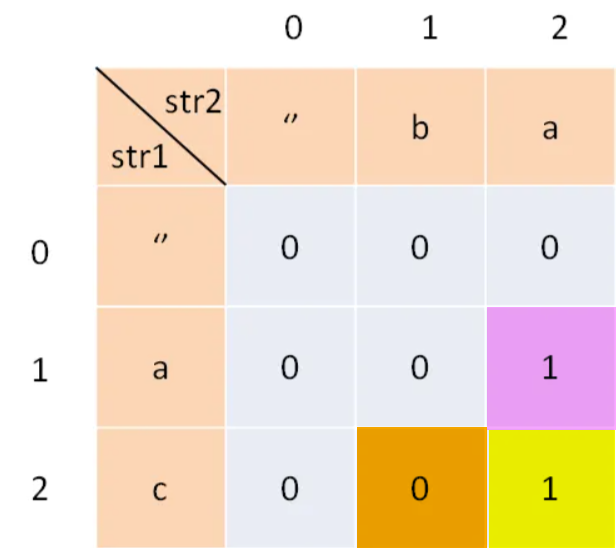
关于这个理论的正确性，从图片中也可以看出来，选择的缺省位置确实是本行、列中的最大值，也映证了 dp 数组确实是具备状态传递的特性的。

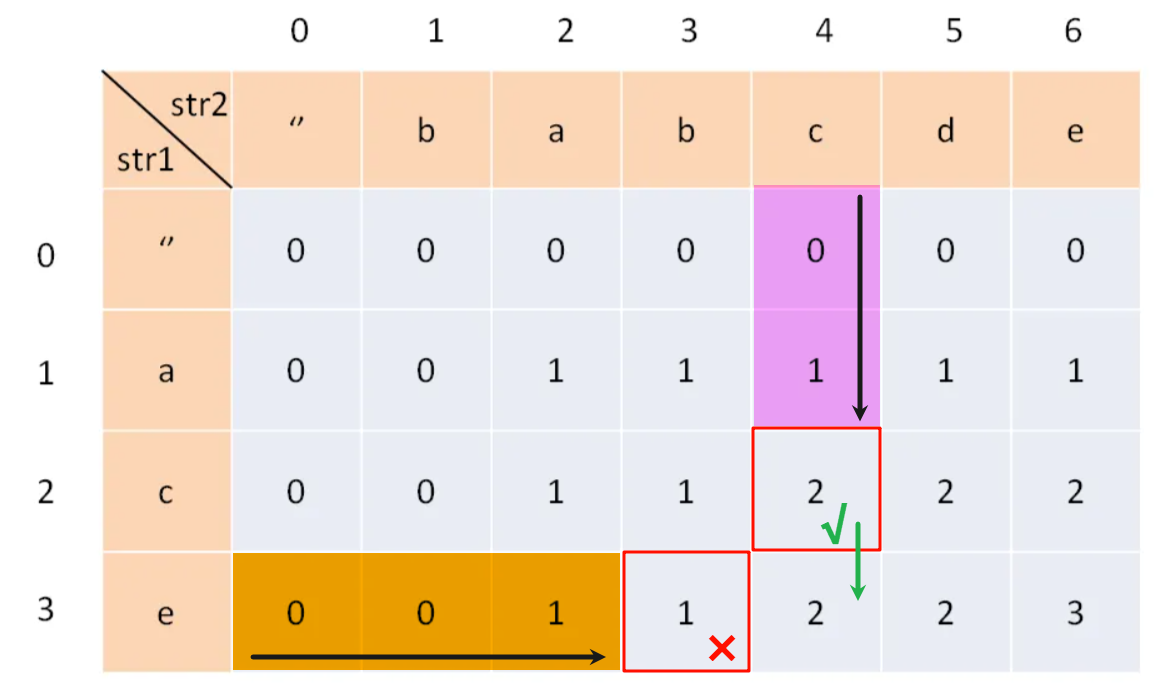
题解如下：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        for (int i = 1; i <= text1.size(); i++) {
            for (int j = 1; j <= text2.size(); j++) {
                if (text1[i - 1] == text2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

诚如上面示意图所示，针对这列比较抽象的题目而言，做一个二维数组的示意图是比较容易帮助理解的，比如针对下面这道题：1035. 不相交的线 - 力扣（LeetCode），我们在没有头绪时先画一个二维数组标一下数字试试：

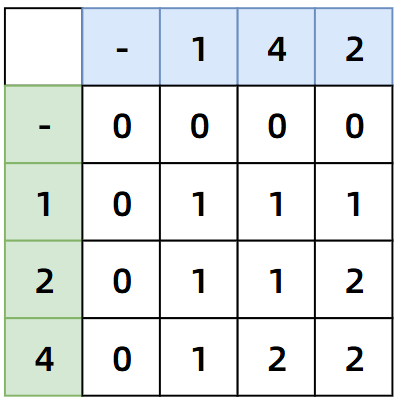
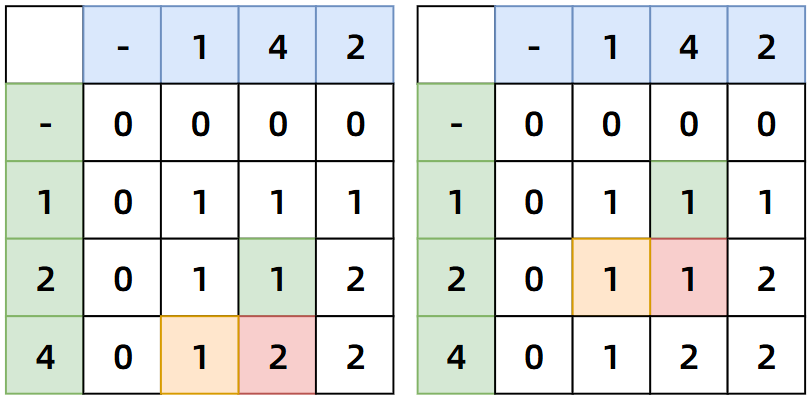
随机选一个格子来推测一下状态转移方程，比如我们选第四行第四列这个 1 来看看，当遍历到14和12时，能产生几条不相交的线呢？由于只有一个数字相同，2 和 4 不等，只能产生一条线。再看看14和124这处格子是如何变为 2 的？由于存在两个数字相等，而且 14中的 1、4 和124中的 1、4 出现的相对位置是一致的，所以能产生两条线，说到相对位置，其实也就是上面的最长公共子序列问题，简直一模一样！

解答如下：

class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));
        for (int i = 1; i <= A.size(); i++) {
            for (int j = 1; j <= B.size(); j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[A.size()][B.size()];
    }
};

番外篇：编辑原字符串

这类问题通常是基于上面的718. 最长重复子数组 - 力扣（LeetCode）和1143. 最长公共子序列 - 力扣（LeetCode）的基础上拓展而来的，举一个例子，比如72. 编辑距离 - 力扣（LeetCode），我们还是先画出二维数组来看看：

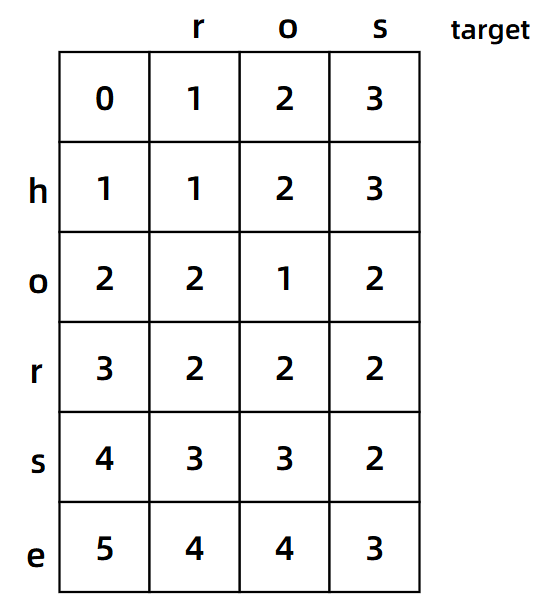
比如我们选择第二行第二列的 1，这个 1 如何得出的？还是之前的看[i][j-1]和[i-1][j]吗？r 和 h 也不相等啊，不妨看看左上角的元素[i-1][j-1]，若当前比较元素不相等，则选出上下和左上元素中的最小者加一。

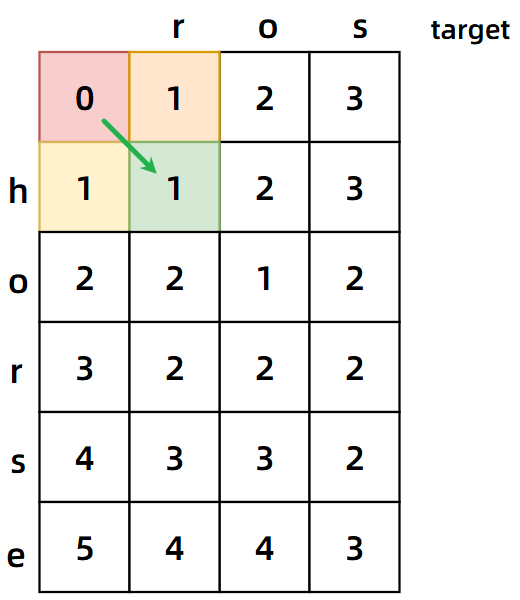
我们再选一个点来看看：

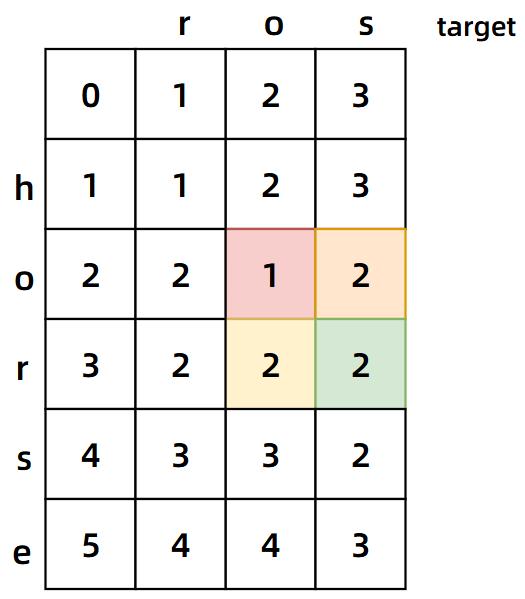
规律仍然存在，说明我们的推测是正确的，得到状态转移方程如下：

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

对于上下和左上元素的形象解释就是分别对当前word1进行删除一个元素、添加一个元素、替换一个元素。

番外篇：涉及到回文的子串/子序列问题

516. 最长回文子序列 - 力扣（LeetCode）

这样的只有一个原串的题目，该怎么画图呢？我们定义本题的 dp 数组含义为：dp[i][j]：从 i 开始到 j 结束的最长回文子序列的长度。尝试着画图如下：

很明显的，数组左下角均为 0，这其实也暗示了本题不能照之前那样考虑上下和左上方的元素了，那我们不妨反其道而行之，看看左、下和左下的元素，很容易看出：

if (s[i] == s[j]) {
    dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}