递归思想
例:查找数组最大值
public class GetMaxValue {
public static int maxValue(int[] arr) {
return f(arr, 0, arr.length - 1);
}
// arr[l....r]范围上的最大值
public static int f(int[] arr, int l, int r) {
if (l == r) {
return arr[l];
}//base case
int m = (l + r) / 2;
int lmax = f(arr, l, m);
int rmax = f(arr, m + 1, r);
return Math.max(lmax, rmax);
}
public static void main(String[] args) {
int[] arr = { 3, 8, 7, 6, 4, 5, 1, 2 };
System.out.println("数组最大值 : " + maxValue(arr));
}
}通过做调用图分析执行流程,可以明晰执行顺序。
递归原理
系统构造一个栈空间
当程序执行到13行时,发现缺少lmax变量的值,于是执行子过程:f(arr,l,m)
系统会将所有临时变量压入栈中,并等待一个结果:lmax,此时原f(3,0)函数已被销毁
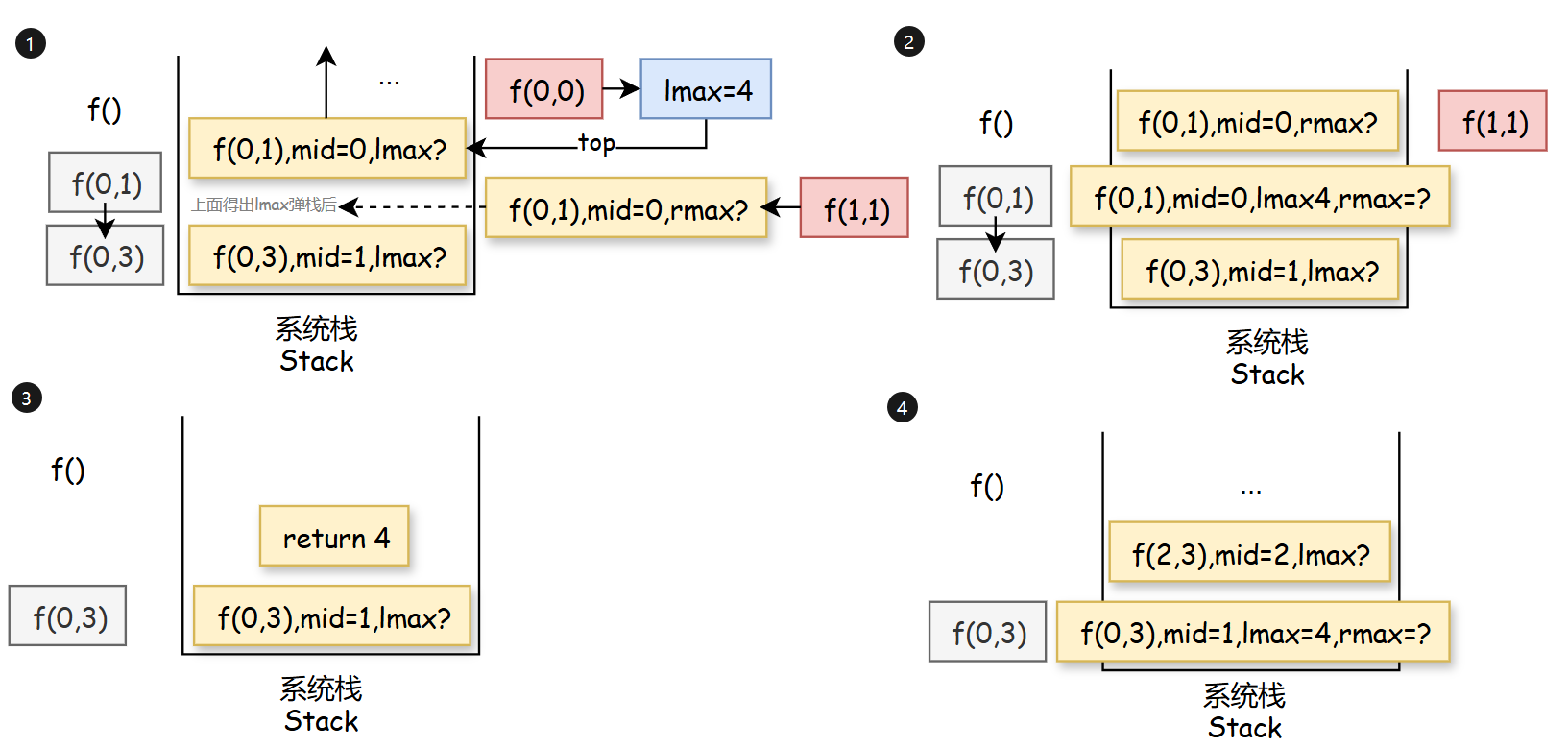
任何递归都可以改为非递归实现:不用系统栈,自己实现栈
递归改为非递归的必要性
- 工程上几乎一定要改,除非确定数据量再大也一定不会造成深递归。比如:归并排序(左分支执行完的空间被右侧使用)、快速排序、线段树、很多的平衡树等
- 算法笔试中,能通过就不改
Master公式
用于计算递归问题的时间复杂度
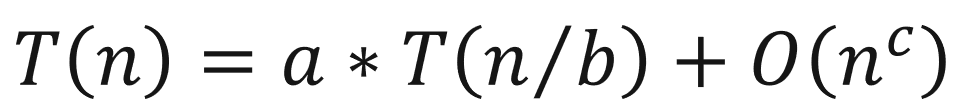
其中,a是调用了几次子过程,b是子过程将数据量减少了多少,c是除子过程外其他操作的时间复杂程度。如果符合上述表达式的格式,且所有子问题规模相同的递归,则该递归过程的时间复杂度为:
- 如果log(b,a) < c,复杂度为:O(n^c)
- 如果log(b,a) > c,复杂度为:O(n^log(b,a)) 以b为底a次方
- 如果log(b,a) == c,复杂度为:O(n^c * logn) N的C次方乘以..
上例中,a=2,b=2,c=0;
时间复杂度为:o(N)
若表达式为:
,则时间复杂度为:
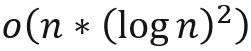

Comments NOTHING