归并排序

归并排序整体过程

左部分排好序
右部分排好序
利用merge过程让左右整体有序

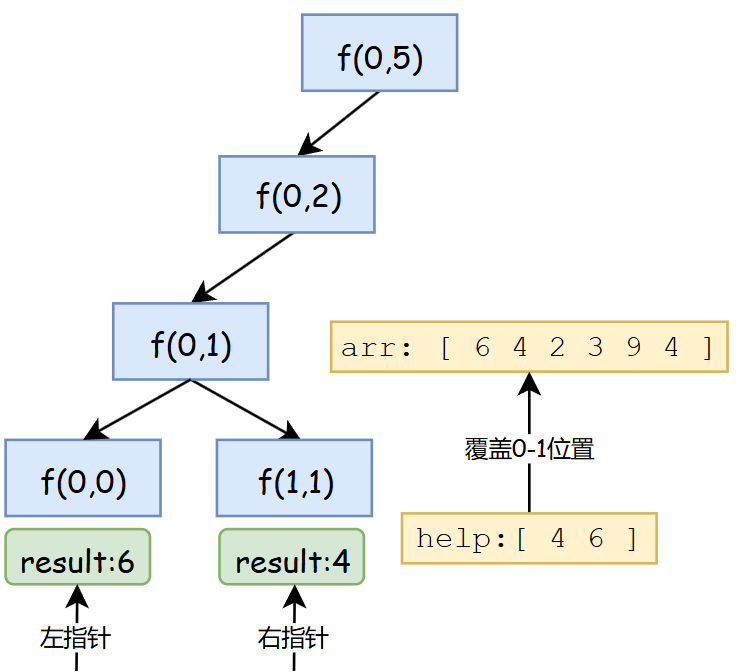
开始merge过程后，利用指针和辅助数组，先将小的数字放入辅助数组直到某一指针为空后（规定：相等时，拷贝左指针所指数字），将另一指针后剩下元素加入数组。这一过程完成后，将辅助数组中元素刷回原数组对应位置。

递归实现：

public class Code01_MergeSort {

    public static int MAXN = 100001;

    public static int[] arr = new int[MAXN];

    public static int[] help = new int[MAXN];

    public static int n;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        in.nextToken();
        n = (int) in.nval;
        for (int i = 0; i < n; i++) {
            in.nextToken();
            arr[i] = (int) in.nval;
        }
        mergeSort1(0, n - 1);
        //mergeSort2();
        for (int i = 0; i < n - 1; i++) {
            out.print(arr[i] + " ");
        }
        out.println(arr[n - 1]);
        out.flush();
        out.close();
        br.close();
    }

    // 归并排序递归版
    // 假设l...r一共n个数
    // T(n) = 2 * T(n/2) + O(n)
    // a = 2, b = 2, c = 1
    // 根据master公式，时间复杂度O(n * logn)
    // 空间复杂度O(n)
    public static void mergeSort1(int l, int r) {
        if (l == r) {
            return;
        }
        int m = (l + r) / 2;
        mergeSort1(l, m);
        mergeSort1(m + 1, r);
        merge(l, m, r);
    }

    // l....r 一共有n个数
    // O(n)
    public static void merge(int l, int m, int r) {
        int i = l;//新进来的数字应该放在什么位置
        int a = l;
        int b = m + 1;
        while (a <= m && b <= r) {
            help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];
        }
        // 左侧指针、右侧指针，必有一个越界、另一个不越界
        while (a <= m) {
            help[i++] = arr[a++];
        }
        while (b <= r) {
            help[i++] = arr[b++];
        }
        for (i = l; i <= r; i++) {
            arr[i] = help[i];
        }
    }

}

非递归实现：

public static void mergeSort2() {
        // 一共发生O(logn)次
        for (int l, m, r, step = 1; step < n; step <<= 1) {
            // 内部分组merge，时间复杂度O(n)
            l = 0;
            while (l < n) {
                m = l + step - 1;
                if (m + 1 >= n) {
                    break;
                }
                r = Math.min(l + (step << 1) - 1, n - 1);
                merge(l, m, r);
                l = r + 1;
            }
        }
    }